Modelarea Gravitatiei, in Rezistenta Materialelor, pe o grinda (plan) incarcata, solicitata la incovoiere
2 participanți
Pagina 1 din 1
 Modelarea Gravitatiei, in Rezistenta Materialelor, pe o grinda (plan) incarcata, solicitata la incovoiere
Modelarea Gravitatiei, in Rezistenta Materialelor, pe o grinda (plan) incarcata, solicitata la incovoiere
.
. Formularea din titlu, aparent bizara, a fost posibila datorita Teoriei Gravitationale elaborate de prof. englez Bruce Harvey.
Unul din exemplele concrete, folosite de acest creator in teoria sa, a fost luat din Rezistenta Materialelor (RM). Am considerat, dupa verificarea calculelor, ca exemplul dat de profesor ar putea sa deschida posibilitati f. interesante de studiu a fortelor gravitationale si de explicare a mecanismului lor de actiune.
Intrucat stiinta RM este foarte exacta, foarte bine verificata in tehnica si f. bine validata de practica, posibilitatea modelarii gravitatiei pe o grinda solicitata la incovoiere prin incarcare cu forte "clasice" (aflate in acelasi plan) mi s-a parut a fi un prilej (neasteptat) de analiza a interactiunii fortelor gravitationale pe modelul fizic al unei grinde solicitate cu forte de incarcare obisnuite. Cu aceasta ocazie ma tin si de cuvantul dat (pe alte saituri), si anume de a elucida/dovedi anume aspecte legate de gravitatie prin intermediul unei astfel de modelari.
De aceea am initiat acest studiu -cu nume bizar- destinat sa dea, pe cat posibil, raspunsuri la intrebari ce-i framanta pe multi cercetatori (amatori) in legatura cu gravitatia. Reusita acestui demers pare sa depinda doar de gradul de conformitate al modelarii, (caci despre modelarea gravitatiei vorbim aici) conformitate ce o vom urmari mereu pe parcursul acestui studiu.
Profesorul B. H. se autoprezinta in saiturile pe care le voi numi in continuare.
http://www.bearsoft.co.uk/index.html
Aceasta prima adresa e cuprinzatoare si am desprins din ea o alta -biografica:
http://www.bearsoft.co.uk/new_site/phys/biog.pdf
Capitolul "Brace Principle" incepe cu schita urmatoare:
.

Fig.1
pe baza careia se desfasoara apoi calculele. Cei interesati au de-acum suficienta documentare "de internet" pentru amanunte suplimentare iar eu voi incepe direct cu rezolvarea unei grinzi.
Aceasta modelare, prima aleasa, e cam departe de ipoteza sinelor din tavan propuse de B.H. dar imi simplifica mult calculele. Pentru inceput, merge.
Semnificatia termenilor din titlu (pentru cei nefamiliarizati cu RM):
simpla rezemare , reazemul simplu, este o notiune clara pentru oricine (aceasta denumire o deosebeste de reazemarea articulata, reazemul articulat);
incovoierea plana - toate sarcinile se afla intr-un singur plan longitudinal, care contine una din axele principale centrale de inertie ale tuturor sectiunilor transversale;
incovoiere simpla - numeste existenta simultana a momentului incovoietor si a fortei taietoare in sectiunile transversale ale grinzii (deosebita de incovoierea pura). Definitiile acestea le-am luat din cartea profesorului meu de RM, Ioan Deutsch dar se gasesc (in mod normal) in toate manualele de RM.


Fig. 2 Grinda simplu rezemata
Prima este depusa pe grinda forta P si ea va produce sagetile v1P si v2P in punctele 1 si 2 de pe grinda (totuna cu punctele de aplicatie ale fortelor P si Q). In mod corespunzator, forta P va produce si lucrul mecanic L1P= 0,5*P*v1P.
Apoi, pe grida deformata deja de P, este asezata forta Q. Ea va produce sagetile v1Q si v2Q in aceleasi puncte, 1 si 2. In mod corespunzator, prin deplasarea fortei P pe distanta (sageata) v1Q se produce lucrul mecanic L1Q= P*v1Q iar forta Q, deplasandu-se pe lungimea (sageata) v2Q, va produce lucrul mecanic L2Q= 0,5*Q*v2Q, in propriul sau punct de aplicare.
Presupunand forta P fixata in punctul 1, dintre cele patru sageti ne va interesa v1Q. Aceasta sageata este "materializarea" actiunii fortei Q asupra fortei P. [Vedem inca din aceasta faza preliminara ca forta Q nu actioneaza in nici un fel asupra fortei P, ci doar asupra grinzii AB producand deformarea fibrei medii a acesteia]
Evident, asimilam energia E1Q unui potential din care, prin derivare in raport cu distanta, putem calcula o forta similara gravitatiei!
[Derivata energiei cu distanta ne da forta; Lucrul mecanic este variatia energiei, in cazul de fata energia initiala a grinzii fiind considerata zero, rezulta ca E1Q este totuna cu variatia de energie si ca atare egala si cu L1Q; acesta fiind si motivul pentru care B.H. se refera doar la Energie, nu si la lucrul mecanic.]
Important este sa subliniem ca (in mod similar, procedand la depunerea fortelor pe grinda in ordine opusa) exista o egalitate intre L1Q si L2P, respectiv intre cele doua forte ce rezulta prin derivarea lor (tot asa precum fortele de atactie dintre doua corpuri ceresti de mase diferite sunt totusi egale). Ma refer in paranteza dinainte la faptul ca logic ar fi daca forta de gravitatie s-ar datora maselor corpurilor -asa cum sustin unii- atunci corpul de masa mai mare ar trebui sa manifeste o forta de atractie mai mare asupra unui corp de masa mai mica.
Aceasta egalitate este f. importanta in RM, avand diferite formulari/aplicatii precum: Teorema lui Betti, Teorema lui Maxwell sau Metoda Mohr-Maxwell. Data fiind importanta acestei egalitati pentru studiul de fata, sa rememoram pe scurt (inclusiv pentru mine):
- Teorema reciprocitatii lucrului mecanic sau teorema lui Betti,
"Daca asupra unui sistem deformabil se aplica doua stari de deformare succesive, lucrul mecanic efectuat de fortele (si cuplurile) din prima stare cu deplasarile (sageti si unghiuri) din a doua este egal cu lucrul mecanic efectuat de fortele din a doua stare cu deplasarile din prima stare de incarcare."
In formule, T. lui Betti suna astfel:
(1) L1P+L2Q+L1Q= L2Q+ L1P+ L2P, de unde rezulta,
(2) L1Q= L2P
In ec. (1), partea stanga a egalitatii este lucrul mecanic al fortelor exterioare aplicate grinzii (din Fig. 2) in succesiunea P mai intai, apoi Q, atunci cand L1P este lucrul mecanic efectuat de forta P in punctul 1 iar P2Q este lucrul mecanic efectuat de forta Q in punctul de aplicatie 2 si L1Q este lucrul mecanic efectuat de forta P in punctul 1 (pe sageata provocata de Q in 1). Partea stanga a egalitatii consemneaza situatia aplicarii fortelor pe grinda in succesiunea: mai intai Q, apoi P iar L2P reprezinta lucrul mecanic efectuat de forta Q in punctul 2 (deplasandu-se pe sageata produsa de fota P in 2).
Ec. (2) fiind chiar T. lui Betti.
- Teorema reciprocitatii deplasarilor sau teorema lui Maxwell (exprimata pe baza Fig.2):
"Deplasarea produsa in sectiunea 1 a unei bare, cand o forta oarecare este aplicata in sectiunea 2, este egala cu deplasarea produsa in sectiunea 2 cand aceeasi forta calca in sectiunea 1." In cazul de fata, v1Q= v2P daca P=Q.
Incep sa ma gandesc daca nu am gresit cu forte diferite...?
1.1. Calculul deformarii v1Q, respectiv a energiei E1Q,
Folosim din comoditate suprapunerea efectelor si formulele din manuale:
(3) v1Q= [Q*x22*b2/6lEI]( 2a/x2+ a/b- a3/x22*b)
De asemenea, pentru simplificarea calculelor, alegem valori numerice pentru grinda, dupa cum urmeaza:
l= 10 m;
a= 2 m;
b= 8- r (deoarece r este variabil, insemnand distanta dintre sarcini);
x2= 2+ r;
Dupa efectuarea calculelor se obtine:
(4) ∆E= E1Q= L1Q= P*v1Q= [P*Q/30*EI](256+ 96r- 24r2+ r3)
Putem obtine prin derivare:
(5) F= dE1Q/dr= [P*Q/30*EI](96- 48r+ 3r2)
La inceput am crezut ca am gresit deoarece formula (5), prin acordarea unor valori lui r, ne da de regula doar rezultate negative. E bine sa fie numai negative pentru ca in mecanica la formula (5) mai apare si semnul minus. Formula corecta este:
(6) F(x)= - dEp(x)/dx
Intr-adevar, energia de deformare acumulata in grinda este o energie potentiala. Lucrurile se schimba la energia cinetica datorita existentei legaturii:
(7) W= ∆Ec= - ∆Ep, unde W este lucrul mecanic. [Fizica, David H. & Robert R., p 176, 177, pentru formulele 6 si 7]
Am facut aceste precizari mai mult pentru mine caci as putea sa uit aceste lucruri pana la urmatoarea recitire dar ele pot fi de folos si celor ce urmaresc aceste calcule.
F este o "forta" pe care o asimilam, in modelarea noastra, "fortei de atractie gravitationale" , P si Q le asimilam maselor M si m din binecunoscuta formula a "atractiei gravitationale", F= KMm/r2.
?1 Constatam ca r se gaseste la puterea a doua in formula (5). Atata doar ca nu se afla la numitor ca in formula atractiei.
Am putea rezolva echivaland prin inversarea 1/F dar pentru acest caz numeric este prematura o asemenea operatie de echivalare. In paranteza cu puteri ale lui r este probabil sa se schimbe respectiv sa apara/dispara din termenii respectivi, functie de valorile numerice folosite.
Important este de asemenea ca produsul E*I (de fapt, E*Iz) poarta numele de rigiditate la incovoiere a barei.
Putem da niste valori distantei r pentru a verifica variatia "fortei" F cu distanta r.
r= 4 m; v= +320/30(Q/EI); F= -48/30(PQ/EI)
r= 5 m; v= +211/30(Q/EI); F= -69/30(PQ/EI)
r= 6 m; v= +184/30(Q/EI); F= -84/30(PQ/EI)
Constatam de aici ca F scade cu distanta r, prin urmare am avut dreptate mai 'nainte propunand inversarea 1/F.
Sa luam in considerare si un alt exemplu numeric:
l= 100 m;
a= 40;
x2= 40+ r;
b= 60- r
Sageata in punctul 1, provocata de sarcina Q aplicata in punctul 2, este:
v1Q= (Q/EI)(288.000+ 2.400r- 180r2+ r3)/15
F= (PQ/15EI)(2.400- 360r+ 3r2)/15
Dam valori pentru r (incepand de la 10 m in sus deoarece aceasta e limita formulei 3, fara a fi o limita reala, fizica):
r= 11 m; v= +293.951Q/15EI; F= -1197PQ/15EI;
r= 15 m; v= +19.1255Q/EI; F= -155PQ/EI;
Prin urmare inregistram aceeasi crestere a lui F cu distanta (si cu patratul distantei), tinand minte ca semnul minus apare in mod gresit datorita erorii mele de scriere a formulei (5).
Se vede de la inceput ca modelarea pe care am facut-o, in principiu se apropie de ipoteza lui B.H. adica a sinelor prinse de tavan. Ne va trebui totusi o modelare mai buna, o incarcare continua, o forta elastica pe toata lungimea grinzii care sa modeleze "mediul", adica tavanul.
1.2. Analiza calculelor din sectiunea "The Brace Principle"
Inainte de a trece la alte calcule trebuie sa examinam ceea ce B.H. ne prezinta in linkul:
http://www.bearsoft.co.uk/Brace.html
privitor la deformarile (combinate ale) arcurilor si ale grinzii.
De la inceput trebuie spus ca acele calcule (poate facute in graba) sunt complect gresite!
In principal, aceasta calculatie se poate reduce la energia de deformatie ce apare intr-un sistem de doua arcuri legate in serie si supuse apoi intinderii cu o greutate agatata la unul din capete. De la inceput, trebuie precizat ca forta de greutate (de 100 N , sa zicem) va fi aceeasi in ambele arcuri (in cazul de fata unul din arcuri este grinda care se deformeaza 1 mm)! Asa este conform manualelor. Chiar daca as avea 10 arcuri B.H., agatate, in serie, succesiv unul de altul si acest lant de arcuri ar fi prins cu un capat in tavan iar la celalalt capat ar fi pusa o greutate de 100 N, forta aceasta va solicita fiecare arc in parte si lantul de arcuri se va alungi cu 10 m. (Dupa rationamentul autorului, ar trebui sa actioneze doar 10 N pe fiecare arc, ceea ce ar fi fost posibil doar daca arcurile ar fi fost legate in paralel!)
D-l B.H., dupa ce propune de la inceput o forta de 100 N pe arc, mai apoi revine si spune: "...but the extension is only 0,999 m and the force only 99,9 N, so that..." ceea ce este gresit, in sensul ca extensia arcului poate fi de 0,999m dar forta din arc ramane 100 N cat a fost de la bun inceput.
Sau, daca afirmatia sa este corecta, nu specifica pe ce se bazeaza.
Urmatorul citat:
"Let us imagine that we have a frame which is 1 metre longer than the un-stretched springs..." ce apare chiar la inceputul expunerii calculului, nu este prea logic, si as fi inteles sensul daca s-ar fi adaugat:
...a frame with springs which is 1 metre...
Am acceptat si varianta ca la masurare se constata 99,9 N apoi am efectuat pana la un punct aceleasi calcule ca B.H., obtinand 49,90005 j si 0,04995 j dar mai departe, cand ar fi trebuit ca sa avem aceesi forta de 99,9 N in cel de-al doilea arc, B.H. a folosit in mod inexplicabil 99,8 N, ceea ce nu se mai potriveste nici in logica propriului sau calcul (sau care mie imi scapa).
[ E posibil sa fi gandit doar teoretic grinda, ea fiind de fapt ... invizibila adica "subintelegand" prin grinda - "eter". Atunci, se pot masura sau sunt vizibile niste efecte, in timp ce altele apartinand eterului, nu.... Dar in RM si mecanica deformarile, fortele, energiile sunt bine lamurite si complect masurabile.
Revenind la cazul in discutie, daca deplasarea totala a punctului de aplicatie al fortei de 100 N este de 1 m, din care sageata grinzii 1 mm iar alungirea arcului 999 mm, atunci putem spune ca lucrul mecanic efectuat de forta de 100 N este 0,5*100*1= 50 j. Aceasta energie de deformatie totala este egala cu suma energiilor de deformatie ale arcului si grinzii. Respectiv,
Et= 50 N= Ea+ Eg= 0,5*100*0,999+ 0,5*100*0,001= 49,95+ 0,05= 50 N
Exceptand cifrele, in rest, "the brace principle" (cu cele cinci puncte ale sale) si celelalte aprecieri ale lui B.H. sunt corecte. Respectiv, energia potentiala acumulata de grinda este mult mai mica decat cea acumulata de arc, suma lor fiind egala cu energia cinetica dezvoltata de forta de 100 N deplasandu-se pe distanta de 1 m, pe directia fortei.
Importanta este constatarea autorului teoriei precum ca nu se poate depozita, acumula, energie decat intr-o legatura, un sistem dual, dipol, bipolar, etc., in care sa existe obligatoriu doua elemente diferite in interactiune. Aceasta observatie se muleaza perfect pe cazul mecanic (unde nu exista actiune fara reactiune si daca actiunea e purtata de un element atunci e necesar un al doilea element care sa manifeste reactiunea). Ca de obicei, exprimarea engleza este mult mai condensata caci "legatura" cuprinde obligatoriu doua elemente si interactiunea dintre ele.
Punctul 5 din "The brace Principle" e o alta exprimare, sinonima cu teorema lui Betti, prin care se subliniaza similitudinile cu formula atractiei - produsul sarcinilor (maselor) cu distanta dintre ele.
Punctul 3 al principiului legaturii e corect in masura in care acele forte sunt egale ca si valoare. Aplicand pe rand cinci forte/sarcini in cele doua puncte de aplicatie, 1 si 2, de pe grinda, obtinem 15 feluri de lucru mecanic, 5 autoefectuate de fiecare forta (cu 1/2 Fv) si alte 10 care au valoare dubla fata de primele 5.
1.3. Rezumat I
Se simte nevoia fixarii, oranduirii ideilor principale, din cand in cand, in uniformitatea unui text mai lung. De aceea voi face acest rezumat, ori de cate ori e necesar, cu efecte pozitive atat in rememorare cat si in cuprinderea "dintr-o privire" a intregului.
*1. Un cercetator, Bruce Harvey, propune o noua Teorie Gravitatiei si semnaleaza o generalitate mai mare decat ne-am astepta a problemei "atractiei" dintre doua corpuri cu particularizare in mecanica corpurilor solide, respectiv in Rezistenta Materialelor, pe cazul banalei grinzi solicitate la incovoiere plana cu doua sarcini concentrate.
*2. Teorema lui Betti, a reciprocitatii lucrului mecanic, permite un paralelism perfect cu atractia gravitationala -si o modelare tehnica de buna calitate- deci permite un studiu "pe un model de laborator" a gravitatiei si nu numai.
*3. Similitudinile sunt:
- Sarcinile P si Q= Masele a doua corpuri;
- Distanta r dintre sarcinile P si Q= Distanta dintre corpuri;
- Lucrul mecanic L1Q=L2P este "sursa" energetica (potentiala) din care se poate obtine prin derivare cu r "Forta de Atractie Modelata" ;
- Grinda este eterul;
- Rigiditatea grinzii, EI, (o posibila similitudine cu rigiditatea eterului) si echivalentul constantei gravitationale.
?2 Nu prea stiu in ce masura poate fi echivalata inversa unei forte cu o (alta) forta??
*4. Pe exemplul numeric, al grinzii simplu rezemate solicitata la incovoiere de doua sarcini concentrate, s-a confirmat puterea doua a lui r dar nu la numitor. Poate va fi necesara o inversare a termenilor pentru a obtine o concordanta mai buna cu AG (atractia gravitationala).
?3*5. Calculele efectuate de B.H. in sectiunea "The brace principle" par sa fie eronate (ori nu le inteleg eu).
?4*6. Calculele numerice de pana acum nu prea arata o variatie a "fortei" cu patratul lui r ci mai degraba o variatie cu r.
?5Mai exacta ar fi o ecuatie a (sagetii) fibrei medii deformate decat suprapunerea de efecte (formule)...
De fapt schita din Fig. 3 si 4 arata situatia inversata: sarcina uniform distribuita, q, reprezinta "legatura", cele doua reactiuni reprezinta sarcinile agatate de B.H. pe sina din tavan, fara ca aceasta inversare sa afecteze in principiu modelarea dar usurand in schimb rezolvarea grinzii.


Fig. 3+ 4
Am ales, tot pentru simplificarea calculelor, situatia unei grinzi simetrice (atat la intervale cat si la incarcari). Ce-i drept aceasta situatie imi limiteaza modelarea pe care o fac dar vom putea estima totusi avantajele si dezavantajele acestei modelari.
Am ales ca metoda de rezolvare "metoda babeasca", din aproape in aproape, realizand dezideratul exprimat la punctul *6 , paragraful 1.3.
2.1. Portiunea A...1
Momentul de incovoiere pe aceasta portiune, incepand (ca origine) din capatul A, este:
(8] MA1= - qx2/2
Ecuatia fibrei medii deformate,
(9) d2v/dx2= - MA1/EI
Din aceasta, prin integrare, obtinem ecuatia rotirii, φ:
(10) φ= dv/dx= (qx3/6+ C1)/EI;
Constanta de integrare, C1, nu poate fi aflata direct din conditiile la limita ale acestei portiuni, fiind necesara o conditie de continuitate a fibrei (egalitate a rotirii in punctul 1 de pe grinda) si va trebui sa aflam acest lucru din ecuatia rotirii scrisa pentru portiunea 1 - 2. Totusi, in avans, pentru a finaliza calculul la punctul 2.1., dam aceasta valoare:
In punctul 1, φA,1= φ1,2= φ1= -qa3/6EI; Deci in 1, la x=a, inlocuind in ec 10, rezulta:
φA,1= φ1= -qa3/6EI= (qa3/6+ C1)/EI. De aici obtinem valoarea constantei de integrare:
C1= -qa3/3; Deci ecuatia rotirilor (10), rescrisa, este:
(11) φ1,A= (qx3/6- qa3/3)/EI= (x3- 2a3)q/6EI
Functia rotirii fiind determinata, o vom putea integra mai departe pentru aflarea ecuatiei sagetilor:
(12) vA,1= (x4/4- 2xa3+ C2)q/6EI
Din conditia la limita, v=0 la x=a, (caci in dreptul reazemului 1 sageta grinzii este, evident, zero) rezulta:
v1= 0= (a4/4- 2a4+C2)q/6EI si, de aici,
C2= 7a4/4
Ecuatia (12) devine:
(13) vA,1= (x4/4- 2xa3+ 7a4/4)q/6EI
Acum putem afla valoarea sagetii din capatul A, inlocuind in ec. (13) pe x cu zero:
vA= 7qa4/24EI
Dupa cum am spus de la inceput, situatia modelata a fost inversata. Astfel, sageata vA, a capatului consolei, A, fata de reazemul 1 este totuna cu sageata punctului 1 -de aplicatie al fortei- fata de capatul A. Pe aceasta distanta, vA, se deplaseaza si forta din pct. 1 (egala cu qa) producand (o parte din) lucrul mecanic ce ne intereseaza pe noi.
2.2 Portiunea 1...2
In Fig. 4 am facut reducerea consolei la momentul si forta reprezentate in punctul 1. Ecuatia de moment:
(14) M1,2= Mr- qax+ qLx/2- qx2/2; unde Mr= Mredus= -qa2/2
M1,2= -qa2/2- qax+2qax- qx2/2= -qa2/2+ qax- qx2/2
Ec. fibrei medii deformate, d2v/dx2= -M1,2/EI= (qa2/2- qax+ qx2/2)/EI;
Ecuatia rotirii:
(15) φ1,2= dv/dx= (qa2x/2- qax2/2+ qx3/6+ C3)/EI
Din conditia de rotire zero de la mijlocul grinzii (simetrice), φ1,2= 0 la x=a, prin inlocuire in (15), rezulta: C3= -qa3/6. In dreptul punctului 1, deci pentru x= 0, vom avea rotirea:
φ1= - qa3/6EI
(Valoare pe care am folosit-o deja, "in avans", in ec. 10, pentru aflarea lui C1). Ecuatia (15) completa, devine:
(16) φ1,2= (qa2x/2- qax2/2+ qx3/6- qa3/6)/EI= (3a2x- 3ax2+x3- a3)q/6EI
Prin integrare, obtinem ecuatia sagetilor:
(17) v1,2= (3a2x2/2- 3ax3/3+ x4/4- a3x+ C4)q/6EI;
Din conditiile de legatura: x= 2a, v1,2= v2= 0 sau x= 0, v1= 0, rezulta C4= 0
Facand in continuare calculul pentru portiunea 2 - B (nu l-am mai inclus aici), am obtinut acelasi rezultat pentru sageata din B, egala cu aceea din A, ceea ce constituie o verificare a calculului.
In ceea ce priveste energia ce ne intereseaza, egala cu lucrul mecanic efectuat de una din forte (reactiune in problema), sa zicem aceea din punctul 1, pe sageata provocata in 1 de forta din 2, vom considera sageata respectiva ca fiind jumatate din vA (sau vB), gratie simetriei perfecte din grinda.
Deci jumatate din vA,1: q*0,5*7*a4/(24*EI)= 7qa4/48EI. Energia potentiala va fi:
(18) E1,2= qa*7qa4/48EI= 7q2a5/48EI;
a= r/2, r fiind distanta dintre sarcini/punctele de aplicatie ale sarcinilor.
E1,2= 7q2r5/(32*48EI) Derivata energiei in raport cu r, va fi "forta de atractie" (presupusa/propusa de noi):
(19) F= dE1,2/dr= 7*5q2r4/(32*48EI)= 35q2r4/(1104EI)
?6 Constatam ca am obtinut o proportionalitate a "fortei" cu puterea a patra a distantei! Destul de departe de ceea ce ne-am propus... In schimb, putem deduce de aici ca in functie de felul incarcarii pe grinda se obtine o "forta" proportionala cu diferite puteri ale distantei, ceea ce ne duce cu gandul la ideea ca alegand o anume incarcare s-ar putea gasi pana la urma o dependenta dorita de noi la modelare, functie de patratul distantei (ori poate chiar de inversul patratului distantei)... Sper ca am calculat bine pana aici.
Mai putem face un artificiu aici, tinand cont ca produsul qr=2qa. In locuindu-l in rezultatul formulei (19), obtinem:
F= 140*q2*a2*r2/1104EI, adica o proportionalitate cu patratul distantei!
?7 Un neajuns al grinzii simetrice este e faptul ca nu putem "micsora" distanta r in raport cu intreaga lungime a grinzii (cu care se afla in raportul fix de 1:4). In acest fel, nu vom putea determina cum ar fi influentata marimea fortei de variatia lui r.
?8 Un alt neajuns: sarcina egal distribuita, q, e o modelare aproximativa a legaturii elastice dintre sine si tavan. Acest neajuns ar putea fi rezolvat cu grinda de lungime infinita plasata pe suport elastic - sinele de cale ferata. La aceasta, suportul elastic e o sarcina distribuita q= -k*v, adica elasticitatea e proportionala cu sarcina de pe sine/grinda.
Calculele acestea de rezistenta pot fi destul de plictisitoare, au multi coeficienti, semne algebrice (si mie imi prilejuiesc nenumarate greseli). Probabil nici nu trezesc interesul (eventualului) cititor. Totusi, pentru fluenta urmaririi expunerii dar si ca principiu, in semn de respect pentru cititori, prezentarea calculelor in amanunt (consider eu) este un gest de elementara politete si o necesitate de comunicare cu ceilalti.
Resimt la randul meu un sentiment neplacut, atunci cand citesc un articol tehnic sau stiintific, o carte sau chiar un manual si vad ca autorul da o formula de inceput, face tot felul de consideratii, dand apoi la sfarsit niste rezultate (poate incomplete). Astfel, nu poti verifica rationamentele pe care le-a facut acel autor, calculele sale, aproximarile inerente si iti pui deseori intrebarea: ce-a vrut sa zica? Chiar trebuie sa-l crezi pe cuvant? Ca principiu, insa, in stiinta si tehnica nu exista "crezutul pe cuvant" ci doar verificarea, macar verificarea calculelor, si, -daca se poate- verificarea experimentala, masurarea, etc.

Referitor la observatia facuta mai sus, privitoare la o distributie neuniforma a "reactiunii" pe grinda reprezentand "sinele lui B.H.", in sensul ca e de asteptat ca in dreptul sarcinilor concentrate (P si Q) reactiunea/deformarea sa fie mai mare sau maxima, descrescand cu distanta de la sarcina inspre capetele "sinelor". Am reprezentat o aproximare liniara (grad I) a acestor distributii de reactiuni in Fig. 5, impunand chiar si conditia de egalitate a reactiunilor cu actiunile:
P= pL/2= pa/2+ p(r+b)/2;
Q= qL/2= qb/2+ q(r+a)/2

Fig. 5. [Gv]
Din pdv al echilibrului mecanic este evident ca aceasta grinda, suspendata elastic de tavan prin intermediul fortelor distribuite "triunghiular", p si q, se gaseste in dezechilibru mecanic pentru ca nu am asigurat -in afara de egalitatea fortelor- si egalitatea momentelor (de rasturnare).
Totusi, experienta de zi cu zi ne spune ca asemenea situatii sunt banal intalnite. Dau aici exemplul unei scanduri intinse peste un teren noroios si pe care paseste o persoana. Persoana odata aflata pe scandura va fi permanent in echilibru (de forte) cu reactiunea terenului noroios dar numai atunci cand persoana ajunge la mijlocul scandurii, sistemul acesta se va afla si in echilibru de momente. Altfel spus, in afara fractiunii de secunda cand persoana traverseaza mijlocul scandurii, in restul parcursului, pe tot timpul deplasarii persoanei pe scandura, sistemul se afla in dezechilibru de momente, constatandu-se tendinta de ridicare a unuia din capetele scandurii.
Acest lucru este mai evident pentru cazul unei persoane ce se deplaseaza de la un capat la altul al unei barci. Greutatea scandurii sau a barcii (prin ridicarea capatului opus) va tinde sa reechilibreze situatia.
- Ce se intampla insa in cazul a doua corpuri ceresti "legate" de eterul inconjurator si care nu au o greutate, precum cea a scandurii sau a barcii, ca sa compenseze dezechilibrul de moment de rotatie (moment de rasturnare, numit mai sus)?
- Pai, se vor roti unul in jurul celuilalt, asa cum se si poate observa astronomic. De fapt, ele nu se rotesc unul in jurul celuilalt ci se rotesc in jurul unui centru comun, ne spun astronomii. Grinda pe care am desenat-o in Fig. 5 (daca reusesc sa realizez acea distributie de forte) chiar acest lucru va face si ea.
?9 S-ar putea determina acest centru de rotatie la grinda din figura?
Aceasta "incarcare in dezechilibru", o nesimetrie functionala, poate ca este cel mai interesant caz de pana aici, a carui studiere ar putea conduce la "revelatii" deosebite in urma unei analize atente.
. Formularea din titlu, aparent bizara, a fost posibila datorita Teoriei Gravitationale elaborate de prof. englez Bruce Harvey.
Unul din exemplele concrete, folosite de acest creator in teoria sa, a fost luat din Rezistenta Materialelor (RM). Am considerat, dupa verificarea calculelor, ca exemplul dat de profesor ar putea sa deschida posibilitati f. interesante de studiu a fortelor gravitationale si de explicare a mecanismului lor de actiune.
Intrucat stiinta RM este foarte exacta, foarte bine verificata in tehnica si f. bine validata de practica, posibilitatea modelarii gravitatiei pe o grinda solicitata la incovoiere prin incarcare cu forte "clasice" (aflate in acelasi plan) mi s-a parut a fi un prilej (neasteptat) de analiza a interactiunii fortelor gravitationale pe modelul fizic al unei grinde solicitate cu forte de incarcare obisnuite. Cu aceasta ocazie ma tin si de cuvantul dat (pe alte saituri), si anume de a elucida/dovedi anume aspecte legate de gravitatie prin intermediul unei astfel de modelari.
De aceea am initiat acest studiu -cu nume bizar- destinat sa dea, pe cat posibil, raspunsuri la intrebari ce-i framanta pe multi cercetatori (amatori) in legatura cu gravitatia. Reusita acestui demers pare sa depinda doar de gradul de conformitate al modelarii, (caci despre modelarea gravitatiei vorbim aici) conformitate ce o vom urmari mereu pe parcursul acestui studiu.
Profesorul B. H. se autoprezinta in saiturile pe care le voi numi in continuare.
http://www.bearsoft.co.uk/index.html
Aceasta prima adresa e cuprinzatoare si am desprins din ea o alta -biografica:
http://www.bearsoft.co.uk/new_site/phys/biog.pdf
Capitolul "Brace Principle" incepe cu schita urmatoare:
.

Fig.1
pe baza careia se desfasoara apoi calculele. Cei interesati au de-acum suficienta documentare "de internet" pentru amanunte suplimentare iar eu voi incepe direct cu rezolvarea unei grinzi.
1* Model: Grinda dreapta, (simplu) rezemata la capete, solicitata la incovoiere plana simpla
Aceasta modelare, prima aleasa, e cam departe de ipoteza sinelor din tavan propuse de B.H. dar imi simplifica mult calculele. Pentru inceput, merge.
Semnificatia termenilor din titlu (pentru cei nefamiliarizati cu RM):
simpla rezemare , reazemul simplu, este o notiune clara pentru oricine (aceasta denumire o deosebeste de reazemarea articulata, reazemul articulat);
incovoierea plana - toate sarcinile se afla intr-un singur plan longitudinal, care contine una din axele principale centrale de inertie ale tuturor sectiunilor transversale;
incovoiere simpla - numeste existenta simultana a momentului incovoietor si a fortei taietoare in sectiunile transversale ale grinzii (deosebita de incovoierea pura). Definitiile acestea le-am luat din cartea profesorului meu de RM, Ioan Deutsch dar se gasesc (in mod normal) in toate manualele de RM.


Fig. 2 Grinda simplu rezemata
Prima este depusa pe grinda forta P si ea va produce sagetile v1P si v2P in punctele 1 si 2 de pe grinda (totuna cu punctele de aplicatie ale fortelor P si Q). In mod corespunzator, forta P va produce si lucrul mecanic L1P= 0,5*P*v1P.
Apoi, pe grida deformata deja de P, este asezata forta Q. Ea va produce sagetile v1Q si v2Q in aceleasi puncte, 1 si 2. In mod corespunzator, prin deplasarea fortei P pe distanta (sageata) v1Q se produce lucrul mecanic L1Q= P*v1Q iar forta Q, deplasandu-se pe lungimea (sageata) v2Q, va produce lucrul mecanic L2Q= 0,5*Q*v2Q, in propriul sau punct de aplicare.
Presupunand forta P fixata in punctul 1, dintre cele patru sageti ne va interesa v1Q. Aceasta sageata este "materializarea" actiunii fortei Q asupra fortei P. [Vedem inca din aceasta faza preliminara ca forta Q nu actioneaza in nici un fel asupra fortei P, ci doar asupra grinzii AB producand deformarea fibrei medii a acesteia]
Evident, asimilam energia E1Q unui potential din care, prin derivare in raport cu distanta, putem calcula o forta similara gravitatiei!
[Derivata energiei cu distanta ne da forta; Lucrul mecanic este variatia energiei, in cazul de fata energia initiala a grinzii fiind considerata zero, rezulta ca E1Q este totuna cu variatia de energie si ca atare egala si cu L1Q; acesta fiind si motivul pentru care B.H. se refera doar la Energie, nu si la lucrul mecanic.]
Important este sa subliniem ca (in mod similar, procedand la depunerea fortelor pe grinda in ordine opusa) exista o egalitate intre L1Q si L2P, respectiv intre cele doua forte ce rezulta prin derivarea lor (tot asa precum fortele de atactie dintre doua corpuri ceresti de mase diferite sunt totusi egale). Ma refer in paranteza dinainte la faptul ca logic ar fi daca forta de gravitatie s-ar datora maselor corpurilor -asa cum sustin unii- atunci corpul de masa mai mare ar trebui sa manifeste o forta de atractie mai mare asupra unui corp de masa mai mica.
Aceasta egalitate este f. importanta in RM, avand diferite formulari/aplicatii precum: Teorema lui Betti, Teorema lui Maxwell sau Metoda Mohr-Maxwell. Data fiind importanta acestei egalitati pentru studiul de fata, sa rememoram pe scurt (inclusiv pentru mine):
- Teorema reciprocitatii lucrului mecanic sau teorema lui Betti,
"Daca asupra unui sistem deformabil se aplica doua stari de deformare succesive, lucrul mecanic efectuat de fortele (si cuplurile) din prima stare cu deplasarile (sageti si unghiuri) din a doua este egal cu lucrul mecanic efectuat de fortele din a doua stare cu deplasarile din prima stare de incarcare."
In formule, T. lui Betti suna astfel:
(1) L1P+L2Q+L1Q= L2Q+ L1P+ L2P, de unde rezulta,
(2) L1Q= L2P
In ec. (1), partea stanga a egalitatii este lucrul mecanic al fortelor exterioare aplicate grinzii (din Fig. 2) in succesiunea P mai intai, apoi Q, atunci cand L1P este lucrul mecanic efectuat de forta P in punctul 1 iar P2Q este lucrul mecanic efectuat de forta Q in punctul de aplicatie 2 si L1Q este lucrul mecanic efectuat de forta P in punctul 1 (pe sageata provocata de Q in 1). Partea stanga a egalitatii consemneaza situatia aplicarii fortelor pe grinda in succesiunea: mai intai Q, apoi P iar L2P reprezinta lucrul mecanic efectuat de forta Q in punctul 2 (deplasandu-se pe sageata produsa de fota P in 2).
Ec. (2) fiind chiar T. lui Betti.
- Teorema reciprocitatii deplasarilor sau teorema lui Maxwell (exprimata pe baza Fig.2):
"Deplasarea produsa in sectiunea 1 a unei bare, cand o forta oarecare este aplicata in sectiunea 2, este egala cu deplasarea produsa in sectiunea 2 cand aceeasi forta calca in sectiunea 1." In cazul de fata, v1Q= v2P daca P=Q.
Incep sa ma gandesc daca nu am gresit cu forte diferite...?
1.1. Calculul deformarii v1Q, respectiv a energiei E1Q,
Folosim din comoditate suprapunerea efectelor si formulele din manuale:
(3) v1Q= [Q*x22*b2/6lEI]( 2a/x2+ a/b- a3/x22*b)
De asemenea, pentru simplificarea calculelor, alegem valori numerice pentru grinda, dupa cum urmeaza:
l= 10 m;
a= 2 m;
b= 8- r (deoarece r este variabil, insemnand distanta dintre sarcini);
x2= 2+ r;
Dupa efectuarea calculelor se obtine:
(4) ∆E= E1Q= L1Q= P*v1Q= [P*Q/30*EI](256+ 96r- 24r2+ r3)
Putem obtine prin derivare:
(5) F= dE1Q/dr= [P*Q/30*EI](96- 48r+ 3r2)
La inceput am crezut ca am gresit deoarece formula (5), prin acordarea unor valori lui r, ne da de regula doar rezultate negative. E bine sa fie numai negative pentru ca in mecanica la formula (5) mai apare si semnul minus. Formula corecta este:
(6) F(x)= - dEp(x)/dx
Intr-adevar, energia de deformare acumulata in grinda este o energie potentiala. Lucrurile se schimba la energia cinetica datorita existentei legaturii:
(7) W= ∆Ec= - ∆Ep, unde W este lucrul mecanic. [Fizica, David H. & Robert R., p 176, 177, pentru formulele 6 si 7]
Am facut aceste precizari mai mult pentru mine caci as putea sa uit aceste lucruri pana la urmatoarea recitire dar ele pot fi de folos si celor ce urmaresc aceste calcule.
F este o "forta" pe care o asimilam, in modelarea noastra, "fortei de atractie gravitationale" , P si Q le asimilam maselor M si m din binecunoscuta formula a "atractiei gravitationale", F= KMm/r2.
?1 Constatam ca r se gaseste la puterea a doua in formula (5). Atata doar ca nu se afla la numitor ca in formula atractiei.
Am putea rezolva echivaland prin inversarea 1/F dar pentru acest caz numeric este prematura o asemenea operatie de echivalare. In paranteza cu puteri ale lui r este probabil sa se schimbe respectiv sa apara/dispara din termenii respectivi, functie de valorile numerice folosite.
Important este de asemenea ca produsul E*I (de fapt, E*Iz) poarta numele de rigiditate la incovoiere a barei.
Putem da niste valori distantei r pentru a verifica variatia "fortei" F cu distanta r.
r= 4 m; v= +320/30(Q/EI); F= -48/30(PQ/EI)
r= 5 m; v= +211/30(Q/EI); F= -69/30(PQ/EI)
r= 6 m; v= +184/30(Q/EI); F= -84/30(PQ/EI)
Constatam de aici ca F scade cu distanta r, prin urmare am avut dreptate mai 'nainte propunand inversarea 1/F.
Sa luam in considerare si un alt exemplu numeric:
l= 100 m;
a= 40;
x2= 40+ r;
b= 60- r
Sageata in punctul 1, provocata de sarcina Q aplicata in punctul 2, este:
v1Q= (Q/EI)(288.000+ 2.400r- 180r2+ r3)/15
F= (PQ/15EI)(2.400- 360r+ 3r2)/15
Dam valori pentru r (incepand de la 10 m in sus deoarece aceasta e limita formulei 3, fara a fi o limita reala, fizica):
r= 11 m; v= +293.951Q/15EI; F= -1197PQ/15EI;
r= 15 m; v= +19.1255Q/EI; F= -155PQ/EI;
Prin urmare inregistram aceeasi crestere a lui F cu distanta (si cu patratul distantei), tinand minte ca semnul minus apare in mod gresit datorita erorii mele de scriere a formulei (5).
Se vede de la inceput ca modelarea pe care am facut-o, in principiu se apropie de ipoteza lui B.H. adica a sinelor prinse de tavan. Ne va trebui totusi o modelare mai buna, o incarcare continua, o forta elastica pe toata lungimea grinzii care sa modeleze "mediul", adica tavanul.
1.2. Analiza calculelor din sectiunea "The Brace Principle"
Inainte de a trece la alte calcule trebuie sa examinam ceea ce B.H. ne prezinta in linkul:
http://www.bearsoft.co.uk/Brace.html
privitor la deformarile (combinate ale) arcurilor si ale grinzii.
De la inceput trebuie spus ca acele calcule (poate facute in graba) sunt complect gresite!
In principal, aceasta calculatie se poate reduce la energia de deformatie ce apare intr-un sistem de doua arcuri legate in serie si supuse apoi intinderii cu o greutate agatata la unul din capete. De la inceput, trebuie precizat ca forta de greutate (de 100 N , sa zicem) va fi aceeasi in ambele arcuri (in cazul de fata unul din arcuri este grinda care se deformeaza 1 mm)! Asa este conform manualelor. Chiar daca as avea 10 arcuri B.H., agatate, in serie, succesiv unul de altul si acest lant de arcuri ar fi prins cu un capat in tavan iar la celalalt capat ar fi pusa o greutate de 100 N, forta aceasta va solicita fiecare arc in parte si lantul de arcuri se va alungi cu 10 m. (Dupa rationamentul autorului, ar trebui sa actioneze doar 10 N pe fiecare arc, ceea ce ar fi fost posibil doar daca arcurile ar fi fost legate in paralel!)
D-l B.H., dupa ce propune de la inceput o forta de 100 N pe arc, mai apoi revine si spune: "...but the extension is only 0,999 m and the force only 99,9 N, so that..." ceea ce este gresit, in sensul ca extensia arcului poate fi de 0,999m dar forta din arc ramane 100 N cat a fost de la bun inceput.
Sau, daca afirmatia sa este corecta, nu specifica pe ce se bazeaza.
Urmatorul citat:
"Let us imagine that we have a frame which is 1 metre longer than the un-stretched springs..." ce apare chiar la inceputul expunerii calculului, nu este prea logic, si as fi inteles sensul daca s-ar fi adaugat:
...a frame with springs which is 1 metre...
Am acceptat si varianta ca la masurare se constata 99,9 N apoi am efectuat pana la un punct aceleasi calcule ca B.H., obtinand 49,90005 j si 0,04995 j dar mai departe, cand ar fi trebuit ca sa avem aceesi forta de 99,9 N in cel de-al doilea arc, B.H. a folosit in mod inexplicabil 99,8 N, ceea ce nu se mai potriveste nici in logica propriului sau calcul (sau care mie imi scapa).
[ E posibil sa fi gandit doar teoretic grinda, ea fiind de fapt ... invizibila adica "subintelegand" prin grinda - "eter". Atunci, se pot masura sau sunt vizibile niste efecte, in timp ce altele apartinand eterului, nu.... Dar in RM si mecanica deformarile, fortele, energiile sunt bine lamurite si complect masurabile.
Revenind la cazul in discutie, daca deplasarea totala a punctului de aplicatie al fortei de 100 N este de 1 m, din care sageata grinzii 1 mm iar alungirea arcului 999 mm, atunci putem spune ca lucrul mecanic efectuat de forta de 100 N este 0,5*100*1= 50 j. Aceasta energie de deformatie totala este egala cu suma energiilor de deformatie ale arcului si grinzii. Respectiv,
Et= 50 N= Ea+ Eg= 0,5*100*0,999+ 0,5*100*0,001= 49,95+ 0,05= 50 N
Exceptand cifrele, in rest, "the brace principle" (cu cele cinci puncte ale sale) si celelalte aprecieri ale lui B.H. sunt corecte. Respectiv, energia potentiala acumulata de grinda este mult mai mica decat cea acumulata de arc, suma lor fiind egala cu energia cinetica dezvoltata de forta de 100 N deplasandu-se pe distanta de 1 m, pe directia fortei.
Importanta este constatarea autorului teoriei precum ca nu se poate depozita, acumula, energie decat intr-o legatura, un sistem dual, dipol, bipolar, etc., in care sa existe obligatoriu doua elemente diferite in interactiune. Aceasta observatie se muleaza perfect pe cazul mecanic (unde nu exista actiune fara reactiune si daca actiunea e purtata de un element atunci e necesar un al doilea element care sa manifeste reactiunea). Ca de obicei, exprimarea engleza este mult mai condensata caci "legatura" cuprinde obligatoriu doua elemente si interactiunea dintre ele.
Punctul 5 din "The brace Principle" e o alta exprimare, sinonima cu teorema lui Betti, prin care se subliniaza similitudinile cu formula atractiei - produsul sarcinilor (maselor) cu distanta dintre ele.
Punctul 3 al principiului legaturii e corect in masura in care acele forte sunt egale ca si valoare. Aplicand pe rand cinci forte/sarcini in cele doua puncte de aplicatie, 1 si 2, de pe grinda, obtinem 15 feluri de lucru mecanic, 5 autoefectuate de fiecare forta (cu 1/2 Fv) si alte 10 care au valoare dubla fata de primele 5.
1.3. Rezumat I
Se simte nevoia fixarii, oranduirii ideilor principale, din cand in cand, in uniformitatea unui text mai lung. De aceea voi face acest rezumat, ori de cate ori e necesar, cu efecte pozitive atat in rememorare cat si in cuprinderea "dintr-o privire" a intregului.
*1. Un cercetator, Bruce Harvey, propune o noua Teorie Gravitatiei si semnaleaza o generalitate mai mare decat ne-am astepta a problemei "atractiei" dintre doua corpuri cu particularizare in mecanica corpurilor solide, respectiv in Rezistenta Materialelor, pe cazul banalei grinzi solicitate la incovoiere plana cu doua sarcini concentrate.
*2. Teorema lui Betti, a reciprocitatii lucrului mecanic, permite un paralelism perfect cu atractia gravitationala -si o modelare tehnica de buna calitate- deci permite un studiu "pe un model de laborator" a gravitatiei si nu numai.
*3. Similitudinile sunt:
- Sarcinile P si Q= Masele a doua corpuri;
- Distanta r dintre sarcinile P si Q= Distanta dintre corpuri;
- Lucrul mecanic L1Q=L2P este "sursa" energetica (potentiala) din care se poate obtine prin derivare cu r "Forta de Atractie Modelata" ;
- Grinda este eterul;
- Rigiditatea grinzii, EI, (o posibila similitudine cu rigiditatea eterului) si echivalentul constantei gravitationale.
?2 Nu prea stiu in ce masura poate fi echivalata inversa unei forte cu o (alta) forta??
*4. Pe exemplul numeric, al grinzii simplu rezemate solicitata la incovoiere de doua sarcini concentrate, s-a confirmat puterea doua a lui r dar nu la numitor. Poate va fi necesara o inversare a termenilor pentru a obtine o concordanta mai buna cu AG (atractia gravitationala).
?3*5. Calculele efectuate de B.H. in sectiunea "The brace principle" par sa fie eronate (ori nu le inteleg eu).
?4*6. Calculele numerice de pana acum nu prea arata o variatie a "fortei" cu patratul lui r ci mai degraba o variatie cu r.
?5Mai exacta ar fi o ecuatie a (sagetii) fibrei medii deformate decat suprapunerea de efecte (formule)...
2* Model: Grinda dreapta, simplu rezemata, sarcina uniform distribuita
De fapt schita din Fig. 3 si 4 arata situatia inversata: sarcina uniform distribuita, q, reprezinta "legatura", cele doua reactiuni reprezinta sarcinile agatate de B.H. pe sina din tavan, fara ca aceasta inversare sa afecteze in principiu modelarea dar usurand in schimb rezolvarea grinzii.


Fig. 3+ 4
Am ales, tot pentru simplificarea calculelor, situatia unei grinzi simetrice (atat la intervale cat si la incarcari). Ce-i drept aceasta situatie imi limiteaza modelarea pe care o fac dar vom putea estima totusi avantajele si dezavantajele acestei modelari.
Am ales ca metoda de rezolvare "metoda babeasca", din aproape in aproape, realizand dezideratul exprimat la punctul *6 , paragraful 1.3.
2.1. Portiunea A...1
Momentul de incovoiere pe aceasta portiune, incepand (ca origine) din capatul A, este:
(8] MA1= - qx2/2
Ecuatia fibrei medii deformate,
(9) d2v/dx2= - MA1/EI
Din aceasta, prin integrare, obtinem ecuatia rotirii, φ:
(10) φ= dv/dx= (qx3/6+ C1)/EI;
Constanta de integrare, C1, nu poate fi aflata direct din conditiile la limita ale acestei portiuni, fiind necesara o conditie de continuitate a fibrei (egalitate a rotirii in punctul 1 de pe grinda) si va trebui sa aflam acest lucru din ecuatia rotirii scrisa pentru portiunea 1 - 2. Totusi, in avans, pentru a finaliza calculul la punctul 2.1., dam aceasta valoare:
In punctul 1, φA,1= φ1,2= φ1= -qa3/6EI; Deci in 1, la x=a, inlocuind in ec 10, rezulta:
φA,1= φ1= -qa3/6EI= (qa3/6+ C1)/EI. De aici obtinem valoarea constantei de integrare:
C1= -qa3/3; Deci ecuatia rotirilor (10), rescrisa, este:
(11) φ1,A= (qx3/6- qa3/3)/EI= (x3- 2a3)q/6EI
Functia rotirii fiind determinata, o vom putea integra mai departe pentru aflarea ecuatiei sagetilor:
(12) vA,1= (x4/4- 2xa3+ C2)q/6EI
Din conditia la limita, v=0 la x=a, (caci in dreptul reazemului 1 sageta grinzii este, evident, zero) rezulta:
v1= 0= (a4/4- 2a4+C2)q/6EI si, de aici,
C2= 7a4/4
Ecuatia (12) devine:
(13) vA,1= (x4/4- 2xa3+ 7a4/4)q/6EI
Acum putem afla valoarea sagetii din capatul A, inlocuind in ec. (13) pe x cu zero:
vA= 7qa4/24EI
Dupa cum am spus de la inceput, situatia modelata a fost inversata. Astfel, sageata vA, a capatului consolei, A, fata de reazemul 1 este totuna cu sageata punctului 1 -de aplicatie al fortei- fata de capatul A. Pe aceasta distanta, vA, se deplaseaza si forta din pct. 1 (egala cu qa) producand (o parte din) lucrul mecanic ce ne intereseaza pe noi.
2.2 Portiunea 1...2
In Fig. 4 am facut reducerea consolei la momentul si forta reprezentate in punctul 1. Ecuatia de moment:
(14) M1,2= Mr- qax+ qLx/2- qx2/2; unde Mr= Mredus= -qa2/2
M1,2= -qa2/2- qax+2qax- qx2/2= -qa2/2+ qax- qx2/2
Ec. fibrei medii deformate, d2v/dx2= -M1,2/EI= (qa2/2- qax+ qx2/2)/EI;
Ecuatia rotirii:
(15) φ1,2= dv/dx= (qa2x/2- qax2/2+ qx3/6+ C3)/EI
Din conditia de rotire zero de la mijlocul grinzii (simetrice), φ1,2= 0 la x=a, prin inlocuire in (15), rezulta: C3= -qa3/6. In dreptul punctului 1, deci pentru x= 0, vom avea rotirea:
φ1= - qa3/6EI
(Valoare pe care am folosit-o deja, "in avans", in ec. 10, pentru aflarea lui C1). Ecuatia (15) completa, devine:
(16) φ1,2= (qa2x/2- qax2/2+ qx3/6- qa3/6)/EI= (3a2x- 3ax2+x3- a3)q/6EI
Prin integrare, obtinem ecuatia sagetilor:
(17) v1,2= (3a2x2/2- 3ax3/3+ x4/4- a3x+ C4)q/6EI;
Din conditiile de legatura: x= 2a, v1,2= v2= 0 sau x= 0, v1= 0, rezulta C4= 0
Facand in continuare calculul pentru portiunea 2 - B (nu l-am mai inclus aici), am obtinut acelasi rezultat pentru sageata din B, egala cu aceea din A, ceea ce constituie o verificare a calculului.
In ceea ce priveste energia ce ne intereseaza, egala cu lucrul mecanic efectuat de una din forte (reactiune in problema), sa zicem aceea din punctul 1, pe sageata provocata in 1 de forta din 2, vom considera sageata respectiva ca fiind jumatate din vA (sau vB), gratie simetriei perfecte din grinda.
Deci jumatate din vA,1: q*0,5*7*a4/(24*EI)= 7qa4/48EI. Energia potentiala va fi:
(18) E1,2= qa*7qa4/48EI= 7q2a5/48EI;
a= r/2, r fiind distanta dintre sarcini/punctele de aplicatie ale sarcinilor.
E1,2= 7q2r5/(32*48EI) Derivata energiei in raport cu r, va fi "forta de atractie" (presupusa/propusa de noi):
(19) F= dE1,2/dr= 7*5q2r4/(32*48EI)= 35q2r4/(1104EI)
?6 Constatam ca am obtinut o proportionalitate a "fortei" cu puterea a patra a distantei! Destul de departe de ceea ce ne-am propus... In schimb, putem deduce de aici ca in functie de felul incarcarii pe grinda se obtine o "forta" proportionala cu diferite puteri ale distantei, ceea ce ne duce cu gandul la ideea ca alegand o anume incarcare s-ar putea gasi pana la urma o dependenta dorita de noi la modelare, functie de patratul distantei (ori poate chiar de inversul patratului distantei)... Sper ca am calculat bine pana aici.
Mai putem face un artificiu aici, tinand cont ca produsul qr=2qa. In locuindu-l in rezultatul formulei (19), obtinem:
F= 140*q2*a2*r2/1104EI, adica o proportionalitate cu patratul distantei!
?7 Un neajuns al grinzii simetrice este e faptul ca nu putem "micsora" distanta r in raport cu intreaga lungime a grinzii (cu care se afla in raportul fix de 1:4). In acest fel, nu vom putea determina cum ar fi influentata marimea fortei de variatia lui r.
?8 Un alt neajuns: sarcina egal distribuita, q, e o modelare aproximativa a legaturii elastice dintre sine si tavan. Acest neajuns ar putea fi rezolvat cu grinda de lungime infinita plasata pe suport elastic - sinele de cale ferata. La aceasta, suportul elastic e o sarcina distribuita q= -k*v, adica elasticitatea e proportionala cu sarcina de pe sine/grinda.
Calculele acestea de rezistenta pot fi destul de plictisitoare, au multi coeficienti, semne algebrice (si mie imi prilejuiesc nenumarate greseli). Probabil nici nu trezesc interesul (eventualului) cititor. Totusi, pentru fluenta urmaririi expunerii dar si ca principiu, in semn de respect pentru cititori, prezentarea calculelor in amanunt (consider eu) este un gest de elementara politete si o necesitate de comunicare cu ceilalti.
Resimt la randul meu un sentiment neplacut, atunci cand citesc un articol tehnic sau stiintific, o carte sau chiar un manual si vad ca autorul da o formula de inceput, face tot felul de consideratii, dand apoi la sfarsit niste rezultate (poate incomplete). Astfel, nu poti verifica rationamentele pe care le-a facut acel autor, calculele sale, aproximarile inerente si iti pui deseori intrebarea: ce-a vrut sa zica? Chiar trebuie sa-l crezi pe cuvant? Ca principiu, insa, in stiinta si tehnica nu exista "crezutul pe cuvant" ci doar verificarea, macar verificarea calculelor, si, -daca se poate- verificarea experimentala, masurarea, etc.
3* Model: Grinda dreapta, simplu rezemata, incarcata in dezechilibru

Referitor la observatia facuta mai sus, privitoare la o distributie neuniforma a "reactiunii" pe grinda reprezentand "sinele lui B.H.", in sensul ca e de asteptat ca in dreptul sarcinilor concentrate (P si Q) reactiunea/deformarea sa fie mai mare sau maxima, descrescand cu distanta de la sarcina inspre capetele "sinelor". Am reprezentat o aproximare liniara (grad I) a acestor distributii de reactiuni in Fig. 5, impunand chiar si conditia de egalitate a reactiunilor cu actiunile:
P= pL/2= pa/2+ p(r+b)/2;
Q= qL/2= qb/2+ q(r+a)/2

Fig. 5. [Gv]
Din pdv al echilibrului mecanic este evident ca aceasta grinda, suspendata elastic de tavan prin intermediul fortelor distribuite "triunghiular", p si q, se gaseste in dezechilibru mecanic pentru ca nu am asigurat -in afara de egalitatea fortelor- si egalitatea momentelor (de rasturnare).
Totusi, experienta de zi cu zi ne spune ca asemenea situatii sunt banal intalnite. Dau aici exemplul unei scanduri intinse peste un teren noroios si pe care paseste o persoana. Persoana odata aflata pe scandura va fi permanent in echilibru (de forte) cu reactiunea terenului noroios dar numai atunci cand persoana ajunge la mijlocul scandurii, sistemul acesta se va afla si in echilibru de momente. Altfel spus, in afara fractiunii de secunda cand persoana traverseaza mijlocul scandurii, in restul parcursului, pe tot timpul deplasarii persoanei pe scandura, sistemul se afla in dezechilibru de momente, constatandu-se tendinta de ridicare a unuia din capetele scandurii.
Acest lucru este mai evident pentru cazul unei persoane ce se deplaseaza de la un capat la altul al unei barci. Greutatea scandurii sau a barcii (prin ridicarea capatului opus) va tinde sa reechilibreze situatia.
- Ce se intampla insa in cazul a doua corpuri ceresti "legate" de eterul inconjurator si care nu au o greutate, precum cea a scandurii sau a barcii, ca sa compenseze dezechilibrul de moment de rotatie (moment de rasturnare, numit mai sus)?
- Pai, se vor roti unul in jurul celuilalt, asa cum se si poate observa astronomic. De fapt, ele nu se rotesc unul in jurul celuilalt ci se rotesc in jurul unui centru comun, ne spun astronomii. Grinda pe care am desenat-o in Fig. 5 (daca reusesc sa realizez acea distributie de forte) chiar acest lucru va face si ea.
?9 S-ar putea determina acest centru de rotatie la grinda din figura?
Aceasta "incarcare in dezechilibru", o nesimetrie functionala, poate ca este cel mai interesant caz de pana aici, a carui studiere ar putea conduce la "revelatii" deosebite in urma unei analize atente.
Ultima editare efectuata de catre mm in Mar Feb 18, 2020 11:07 am, editata de 8 ori
mm- Mesaje : 211
Data de înscriere : 12/01/2011
 Re: Modelarea Gravitatiei, in Rezistenta Materialelor, pe o grinda (plan) incarcata, solicitata la incovoiere
Re: Modelarea Gravitatiei, in Rezistenta Materialelor, pe o grinda (plan) incarcata, solicitata la incovoiere
La semnul de intrebare 7 (?7) raspunsul este ca distanta r se poate micsora, dar nu in formulele finale de calcul ci reluand calculul de la inceput, de fiecare data cand se schimba r. Trebuie sa verific cum variaza valoric "atractia" f. de r.
"Modelul in dezechilibru" a fost o idee aparuta in ultima instanta si inca nu o inteleg nici eu.
- Ce-i drept, distributia de reactiuni de forma triunghiulara se poate realiza efectiv dar f. probabil cu o grinda de rigiditate variabila...
- Daca grinda e suspendata elastic in tavan pe un sir des de (arculetze) atunci momentul dezechilibrat imi va ridica capatul mai usor incarcat si arculetele isi vor pierde intinderea (pe care am desenat-o eu, presupunand-o gresit) si unele chiar vor fi comprimate ceea ce va duce la o alta stare de incarcare pe grida, diferita de cea initial presupusa de mine in Fig. 5.
- In acelasi timp, pozitionarea spatial-astronomica a problemei ar putea ramane valabila, gandindu-ma la fluxurile de eter. De fapt acesta si este motivul pentru care am promovat acest model.
Nu pare prea clara dependenta "atractiei" de distanta. E sau nu e patratul distantei? E realizabil oare un model numai cu un termen -r2? Cam multe raspunsuri de dat -inclusiv la precedentele 7 intrebari...
La semnul de intrebare 9, raspunsul e da.
"Modelul in dezechilibru" a fost o idee aparuta in ultima instanta si inca nu o inteleg nici eu.
- Ce-i drept, distributia de reactiuni de forma triunghiulara se poate realiza efectiv dar f. probabil cu o grinda de rigiditate variabila...
- Daca grinda e suspendata elastic in tavan pe un sir des de (arculetze) atunci momentul dezechilibrat imi va ridica capatul mai usor incarcat si arculetele isi vor pierde intinderea (pe care am desenat-o eu, presupunand-o gresit) si unele chiar vor fi comprimate ceea ce va duce la o alta stare de incarcare pe grida, diferita de cea initial presupusa de mine in Fig. 5.
- In acelasi timp, pozitionarea spatial-astronomica a problemei ar putea ramane valabila, gandindu-ma la fluxurile de eter. De fapt acesta si este motivul pentru care am promovat acest model.
Nu pare prea clara dependenta "atractiei" de distanta. E sau nu e patratul distantei? E realizabil oare un model numai cu un termen -r2? Cam multe raspunsuri de dat -inclusiv la precedentele 7 intrebari...
La semnul de intrebare 9, raspunsul e da.
Ultima editare efectuata de catre mm in Lun Iun 06, 2011 11:26 am, editata de 2 ori
mm- Mesaje : 211
Data de înscriere : 12/01/2011
 Re: Modelarea Gravitatiei, in Rezistenta Materialelor, pe o grinda (plan) incarcata, solicitata la incovoiere
Re: Modelarea Gravitatiei, in Rezistenta Materialelor, pe o grinda (plan) incarcata, solicitata la incovoiere
mm, pana acum ai obtinut modelare de gravitatie la care dependenta "fortei de gravitatie" de distanta "r" se face doar cu polinoame in r de gradul 2 (sau 4, n-am inteles prea bine), deci nu ai o dependenta de r2, pura, fara alti termeni de grade inferioare.
Nu prea am inteles incarcarea din Fig. 5. Cum o realizezi daca chiar tu spui ca mecanic e instabila iar din pdv al RM nici nu se pune problema (existentei si rezolvarii unei asemenea incarcari)?
Nu prea am inteles incarcarea din Fig. 5. Cum o realizezi daca chiar tu spui ca mecanic e instabila iar din pdv al RM nici nu se pune problema (existentei si rezolvarii unei asemenea incarcari)?
 Re: Modelarea Gravitatiei, in Rezistenta Materialelor, pe o grinda (plan) incarcata, solicitata la incovoiere
Re: Modelarea Gravitatiei, in Rezistenta Materialelor, pe o grinda (plan) incarcata, solicitata la incovoiere
A rezultat o dependenta [F(r)] de forma unui polinom de grd. II pentru grinda incarcata cu doua forte concentarate, polinom de grd. III pentru grinda incarcata cu forta uniform distribuita si polinom de grd. IV pentru grinda incarcata cu forta distribuita de forma triunghiulara. Sper sa pot obtine si o dependenta de forma unui monom de acelasi grad.
Se poate realiza distributia din Fig. 5 si ne putem imagina ca locul fiecarei sageti din figura va fi luat de niste mini-rachete a caror forta de propulsie este reglata sa fie proportionala cu marimea sagetii inlocuite.
Intrucat "rachetele" P si Q echilibreaza suma propulsiilor mini-rachetelor distribuite, ansamblul grinda+ rachete nu va avea miscare de translatie.
In schimb, datorita existentei perechilor in interactiune (acea "legatura" (brace) de care vorbeste B.H.), pot apare momente de rotatie. In spatiu doua corpuri ceresti se pot roti unul in jurul celuilalt tocmai datorita unui astfel de dezechilibru de momente. O asemenea grinda, aici, se va roti in planul fortelor, asemenea unei moristi si acest lucru se poate materializa si cu numai doua ajutaje paralele, montate pe o bara, indreptate in acelasi sens, cu forte de reactie diferite. Diferenta de forte va face din bara o morisca.
Problema este: care e mecanismul prin care ia nastere rotatia intr-o pereche? Aici se poate medita asupra cauzei...
2.3. Voi remedia neajunsul de la intrebarea (?7), pornind calculele de la capat, pe aceeasi Fig. 3+ 4, (devenite Fig. 3'+4'), cu modificarile:
- in locul celor doua cote "a", dintre capete si fortele concentrate, va fi 2a- r;
- in locul cotei dintre fortele concentrate, r= 2a va fi 2r;
- L= 4a (am lasat aceeasi lungime totala);
- in Fig.4 in locul fortelor concentrate din punctul 1, (2qa si qa), va fi o singura forta qr indreptata in sus;


Fig. 3'+ 4'
- Mred din Fig. 4' va fi: (20) Mred= -q(2a- r)2/2,
restul datelor de intrare ramanand neschimbate (daca nu specificam modificarile ar fi trebuit alte desene). Rezolvam la fel ca la paragrafele 2.2. si 2.1.,
(21) M1,2= Mred+ qrx- qx2/2 = -q(2a- r)2/2+ qrx- qx2/2
(22) d2v/dx2= -M1,2/EI= q(2a- r)2/2- qrx+ qx2/2= [(2a- r)2- rx+ x2/2]q/EI
(23) φ1,2= dv/dx= [(2a-r)2x/2 - rx2/2+ x3/6]q/EI+ C3
Din conditia de rotire zero, φ1,2=0, la mijlocul grinzii, x= r, rezulta prin inlocuire:
(24) C3= [2r3- 3r(2a- r)2]q/6EI
Putem calcula acum valoarea rotirii in nodul 1, pentru x=0 (deoarece avem intreaga ecuatie):
(25) φ1= C3= [2r3- 3r(2a- r)2]q/6EI
Ne mutam cu calculul pe portiunea A - 1:
(26) MA,1= - qx2/2; d2v/dx2= -MA,1/EI= +qx2/2EI
Integram pentru a obtine ec. rotirii si ec sagetii:
(27) φA,1= qx3/6EI+ C1 si
(27b) vA,1= qx4/24EI+ C1x+ C4
Gasim constanta de integrare C1 din conditia de continuitate a rotirii in nodul 1:
pentru x=2a- r, φ1,2= φ1= C3 si obtinem:
(28) C1= [2r3- 2(a+ r)(2a- r)2]q/6EI
Determinam constanta de integrare din conditia ca in nodul 1 sageata este zero, pentru x= 2a-r, pe care le inlocuim in ecuatia sagetii:
(29) C4= [-(2a- r)4- (2a- r)8r3+ 8(a+ r)(2a- r)3]q/24EI
In ecuatia sagetii, din conditia x= 0 rezulta valoarea sagetii (capatului de grinda, pe care o cautam prin acest calcul), care este egala cu termenul liber, C4.
(30) vA= C4= [-(2a- r)4- (2a- r)8r3+ 8(a+ r)(2a- r)3]q/24EI
In aceasta ecuatie putem da orice valori lui r deci putem trasa o curba a variatiei sagetii (in consecinta si a Energiei si a "Fortei") functie de distanta dintre cele doua reactiuni (de fapt echivalentele maselor din gravitatie). Ar trebui ca prin inlocuire cu r= a sa obtinem aceeasi valoare a sagetii ca in rezolvarea de la punctul 2.1. adica,
vA= 7qa4/24EI.
vA= [-(2a-a)4- (2a- a)8a3+ 8(a+ a)(2a- a)3]q/24EI= [-a4- 8a4+ 16a4]q/24EI= 7a4q/24EI,
adica acelasi rezultat ceea ce reprezinta o buna verificare a formulei si calculelor (in care usor se pierde un semn, o cifra, o litera, etc.). Acum putem determina/aprecia numeric aceasta variatie:
Pentru r=a, vA= 7[a4/24EI]= 7k;
r= 0,01a; vA= 48k;
r= 0,10a; vA= 47,31k;
r= 0,30a; vA= 42,23k;
r= 0,50a; vA= 34,53k
Intr-adevar, la o micsorare a distantei r de 10 ori, sageata nu creste de 100 ori (cat ar fi fost cu r2) ci numai de 6,7 ori.
(?10) E posibil sa fi gresit calculele/estimarile privind "forta" pe la sfarsitul paragrafului 2.2. si nu numai. Reiau de la ecuatia vA.
Lucrul mecanic efectuat de una din fortele "de reactie", qa, pe jumatate din valoarea sagetii din A, va fi:
(31) LA= qa*vA/2= qa*[-(2a- r)4- (2a- r)8r3+ 8(a+ r)(2a- r)3]q/48EI[/b]
Derivata lucrului mecanic va fi "forta" pe care o cautam:
(32) F= - dLA/dr= (4r3- 96ar2+ 144a2r)q2a/48EI
Valorile calculate -si comparate- de mai sus erau o estimare "prescurtata" ale "fortei", tinand cont ca in expresia lucrului mecanic doar v este variabila. Acum avem expresia matematica, functia, fortei F. In aceasta ecuatie ii dam lui "r" din nou aceleasi valori ca mai sus:
r= a; F= 52{q2a/48EI}= 52k;
r= 0,5a; F= 48,5k;
r= 0,3a; F= 34,7k;
r= 0,25a; F= 30k;
r= 0,1a; F= 13,4k;
r= 0,001a; F= 1,45k
* Aprecierile mele de mai sus erau usor gresite; situatia corect exprimata (si "neprescurtata"), exprimata sintetic, suna astfel: la micsorarea distantei r de 10 ori (de la a la 0,1a), inversul lui F (am mai amintit despre necesitatea inversarii acestui termen) va creste doar de ~4 ori.
* Arata mai rau decat ma asteptam; Este relativa alegerea valorii r ca referinta; Dependenta lui F de r este slaba (in comparatie cu dependenta cu 1/r2 de la gravitatie)
* Gradul trei al polinomului (al functiei de dependenta) nu are nici o semnificatie cat de cat in rezultatul final din pricina celorlalti termeni.
* Adevarul este ca distantele cosmice de interactie/actiune gravitationala/ pot fi foarte mari comparativ cu distanta intre 2 corpuri dintr-un sistem... Pentru ca sa ma situez in modelarea mea pe aproape trebuie sa folosesc valori mult, mult mai mici pentru r, comparativ cu a.
r= 0,0001a; F= 0,0144k;
r= 0,00001a; F= 0,00144k
Prin urmare, pe aceasta portiune de curba, singurul termen important din polinom devine 144a2r iar acesta are puterea I a lui "r" - distanta dintre "corpuri". E ceva mai bine si era de asteptat ca raportul dintre distanta r si lungimea totala a grinzii sa afecteze rezultatele modelarii.
* Apare inca o conditie: proportiile trebuie alese apropiate de cele gravitationale stiute.
[Teoria spune ca forta de atractie se intinde la infinit dar nimeni nu poate dovedi acest lucru, astfel ca pentru distante foarte mari (dar nu infinite) nici formula atractiei nu sufera abateri perceptibile.]
* Rezultatele sunt inca departe. Modelarea trebuie continuata cu grinda de lungime infinita. O aproximare (grosolana) a acesteia am inceput-o deja folosind "incarcarea triunghiulara".


Fig. 6. [Gv]
In Fig. 6 avem un model ce aproximeaza actiunea unei forte concentrate pe mijlocul unei grinzi aflate pe un teren "moale", unde apare o reactiune distribuita de forma triunghiulara (aproximata in acest fel de mine). [Desenul arata inversat deoarece imi vine mai usor sa-l rezolv in aceasta pozitie rasturnata.]
(33) M1,2= - [(qx)*x/2]*x/3= -(qx/a)*x2/6= - qx3/6a;
Unde, (34) qx= qx/a, qx fiind valoarea sarcinii distribuite in punctul x, la distanta x de origine (capatul 1). Ecuatia fibrei medii deformate:
(34) d2v/dx2= - M1,2/EI= qx3/6a; Prin integrare obtinem ecuatia rotirii:
(35) φ1,2= - (q/6aEI)x4/4+ C1 ; Din conditia x= a; φ= 0, gasim valoarea constantei de integrare:
(36) C1= - qa3/24EI; Ecuatia rotirii e acum determinata:
(37) φ1,2= - (q/24aEI)x4- qa3/24EI; Prin integrare rezulta ec. sagetii:
(38) v1,2= (q/24aEI)x5/5- (qa3/24EI)x+ C2
Din conditia la limita, x=a; v=0, rezulta:
(39) C2= qa4/30EI. Cu aceasta, ecuatia sagetii devine:
(40) v1,2= (q/24aEI)x5/5- (qa3/24EI)x+ qa4/30EI= (q/120aEI)[x5- 5a4x+ 4a5]
Inlocuim variabila x cu (a-r) in ecuatia sagetii pentru a obtine aceeasi sageata, din punctul "curent", dar ca si functie de "r". Dupa cum se vede din Fig.6, aceasta distanta r dintre aplicatiile a doua forte (egale) este aceea care ne intereseaza (si, in final vom studia variatia lui r, valoric).
(41) vr= (q/120aEI)[(a-r)5- 5a4(a- r)+ 4a5]
Energia potentiala, egala cu lucrul mecanic efectuat de catre una din incarcarile qa, deplasandu-se vertical pe distanta vr, este:
(42) ΔE= L= qavr Forta pe care o cautam, echivalentul celei gravitationale:
(43) F= - dE/dr= (q2/120EI)(5r4- 20ar3+ 30a2r2- 20a3r)= (q2/24EI)( r4- 4ar3+ 6a2r2- 4a3r)
Verificare:
In ecuatia (40), sageata ca functie de x,
- pentru x=r trebuie sa rezulte sageata zero (caci reazemul e fix); Prin inlocuire in (40):
v1,2= (q/120aEI)[r5- 5a4r+ 4a5]= 0; Corect!
- pentru x= 0 trebuie sa avem sageata maxima, v≠ 0; Prin inlocuire, primii doi termeni din paranteza se anuleaza si obtinem:
v1,2= (q/120aEI)[ (0)5- 5a4*(0)+ 4a5]= qa4/24EI≠ 0 ; Corect!
In ecuatia (41), sageata functie de r,
- pentru r= 0, ar trebui sa rezulte sageata zero; Inlocuim in ec. (41) si obtinem:
vr= (q/120aEI)[(a-0)5- 5a4(a- 0)+ 4a5]= (q/120aEI)[a5- 5a4a+ 4a5]= 0; Corect!
- pentru r= a, pe capatul grinzii ar trebui sa rezulte o sageata diferita de zero. Inlocuim in ec. (41) pe r cu a, primii doi termeni se anuleaza, si obtinem:
vr= (q/120aEI)[(a-a)5- 5a4(a- a)+ 4a5]= qa4/24EI≠ 0; Corect!
In ec. (43) a derivatei, pentru r= 0, derivata se anuleaza, cum era si normal [caci derivata intai e tangenta la curba si aici, pe reazem, -stim din RM- unghiul tangentei la fibra deformata e zero] iar in aceeasi ec. (43) inlocuind r=a, rezulta o derivata diferita de zero [corespunzand cu ce stim apriori din RM- ca tangenta la curba este diferita de zero]
A trebuit sa ma asigur ca ecuatiile obtinute sunt exacte deoarece la calculele de acest tip apar nenumarate greseli algebrice, din neatentie, din cauza specificului, si - cateodata- din nestiinta. Acum putem da valori numerice (in ec. 43) pentru r cu scopul trasarii diagramei (alta verificare):
r= a; F= -(q2/120EI)5a4= -q2a4/24EI= -k ;
r= 0,8a; F= -0,998k
r= 0,6a; F= -0,974k
r= 0,5a; F= -0,9375k;
r= 0,4a; F= -0,8404k;
r= 0,3a; F= -0,768k;
r= 0,2a; F= -0,592k;
r= 0,1a; F= -0,364k;
r= 0,01a; F= -0,0394k;
r= 0,001a; F= -0,00399k;
r= 0,0001a; F= -0,000399k;
r= 0,00001a; F= -0,0000399k; etc.
Si de aceasta data, la un raport r/a apropiat de cel cosmic, "F" este proportionala cu "r" (la o scadere de 10 ori a lui r, F scade tot de 10 ori). Deci F nu e proportionala cu patratul lui "r", adica patratul distantei dintre punctele de aplicare a sarcinilor.
Ma incurca semnul minus, despre care nu stiu cum a aparut...


Fig. 7.
Grinda asezata pe un mediu elastic este o grinda static nedeterminata.
Mediul, terenul pe care este asezata grinda se considera perfect elastic, adica el coboara sub sarcina si revine dupa inlaturarea sarcinii. E cazul sinelor de cale ferata.
Se considera ca reactiumea din dreptul unei sectiuni oarecare a grinzii, pe care terenul o exercita asupra grinzii, este proportionala cu sageata grinzii din dreptul sectiunii respective (ipoteza E. Winkler). Astfel, reactiunea pe o unitate de lungime a grinzii este:
Rezolvarea acestei grinzi, cu o forta concentrata P, este data in manualul de RM al prof. Ioan Deutsch, de unde aflam ecuatia sagetii v la distanta x de punctul de aplicatie al fortei concentrate:
(44) vx= e-βx(cosβx+ sinβx)P/(8β3EI)
Cu aceasta formula -pe principiul suprapunerii efectelor- putem calcula energia potentiala, inmagazinata de grinda, egala cu lucrul mecanic produs de o a doua forta P, -situata la distanta r (x in formula 44) de prima forta P- ce se deplaseaza pe o distanta egala cu sageata produsa de prima forta P (sau viceversa). [In exemplul numeric din manual, fortele aplicate nu sunt identic egale dar sunt apropiate valoric deci putem folosi forte diferite.]
(45) E= L= Pvr
Forta pe care o cautam e derivata energiei:
(46) F= -dE/dr= P2e-βrsinβr/(4β2EI)
Pe aceasta formula putem determina forma curbei de dependenta, F(r), dand valori lui r. Din pacate nu putem decat presupune valorile coeficientului β. La sinele de cale ferata, in exemplul din manual, produsul βr= 0,742, deci e subunitar. Asta inseamna ca valoarea coeficientului β este comparabila cu distanta r.
A trasa diagrama F(r) e sinonim cu a trasa functia: f= sinβr/eβr
Presupunem β= 0,0053 cm-1
r= 10 cm; βr= 0,053; f= 0,0502;
r= 14 cm; βr= 0,0742; f= 0,069;
r= 100 cm; βr= 0,530; f= 0,297;
r= 140 cm; βr= 0,742; f= 0,238;
r= 500 cm; βr= 2,65; f= 0,033;
r= 600 cm; βr= 3,18; f= -0,0015;
r= 1000 cm; βr= 5,3; f= -0,004;
r= 1200 cm; βr= 6,36; f= 0,00013;
r= 14000 cm; βr= 7,42; f= 0,000543;
Nu am fost prea atent caci aceasta curba era deja trasata in manualele de RM si arata astfel:


Fig. 8.
Functia f este η3 din diagrama.
Problema care apare aici este legata de constatarea ca pentru r=0 functia f=0= kF. Intrucat F ar trebui sa fie modelul fortei de atractie gravitationale, atunci nu se potriveste de loc cu valorile obtinute [in sensul ca "forta" ar trebui sa fie maxima tocmai la r= 0]. Problema aceasta provine din faptul ca am neglijat aspectul/neajunsul enuntat in intrebarile ?1 si ?2. Incerc sa rezolv acest aspect:
Atat in formula (5) de la Modelul 1. cat si in formulele (19) si (32) de la Modelul 2. dar si in formula (43) de la Modelul 3. persista aceasta nepotrivire. Toate aceste formule pot fi sintetizate intr-o singura formula astfel:
(47) F= P*Q*f(r)/k; Putem inversa aceasta relatie:
(48) 1/F= k(1/P)*(1/Q)*(1/f(r)); Facem urmatoarea notatie: 1/F= G; 1/P= M1; 1/Q= M2 si vom obtine urmatoarea relatie (aproape identica cu formula atractiei gravitationale):
(49) G= kM1*M2*(1/f(r))
Daca numitorul f(r) ar fi x2 atunci formal ar fi vorba despre aceeasi formula si modelul ar fi perfect viabil. Pana acum nu am indeplinit inca ultima cerinta: f(r), care uneori e un polinom de gradul 2 in x sau de alt grad, adica nu are forma unui monom, x2. Chiar si cu polinoame, dependenta ce o cautam e ~liniara de grd. I (pe portiunea din curba ce ne intereseaza, la un anume raport r/a).
Ceea ce nu am analizat pana acum este anularea in origine la formula (46) [si la (43), (32), si (19), mai putin la formula (5)] ceea ce este echivalent cu
G= ∞, adica exact cum se intampla in formula gravitatiei [atunci cand r= 0, forta de atractie gravitationala tinde spre ∞]. Sa fi gresit ceva in formula (5)...?
De remarcat ca, in Fig.8, η3 e singura care se anuleaza in origine.
De la sine apare observatia -chiar daca nu are legatura cu modelul nostru- ca valorile folosite in practica (momentul de inertie al sinelor de cale ferata, coeficientul de tasare, coeficientii) conduc la situarea problemei pe curba η3 exact in punctul ei de minim ceea ce nu poate fi o intamplare. Sa fie explicatia ca acolo e "punctul slab" si toate masurile sunt luate pentru dimensionare special pentru zona aceea?...
(?11) Rezultatele formulelor (19) si (32) nu coincid. Trebuie lamurit de ce "nu".
Reprezentarea grafica a functiilor, determinate in cadrul celor catorva modele, poate ajuta la vizualizarea legaturii, la gasirea eventualelor greseli de calcul numeric, la verificare in general, prezentare sintetica de rezultate, etc., fiind si una din cele mai frecvent folosite metode ingineresti. Am reprezentat functia F cat si inversa ei, G. Scarile alese sunt aleatorii pentru fiecare curba trasata.
Fig. 9.?

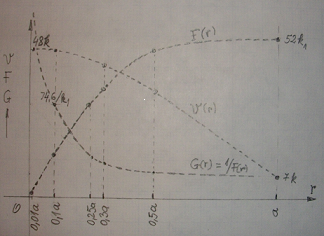
[F. 10 Gv]

Fig.10. [F. 11 Gv]


Fig.12. [Gv]


Fig.13. [Gv]
Fig. 9 (si 12) se refera la Modelul 2*, Fig. 10 se refera la Modelul 5* iar Fig 13 se refera la Modelul 4*. Fig. 12 este o repetare "mai artistica" a Fig. 9.
In Fig. 10 se confirma forma de sinusoida amortizata a functiei f. Functia g(r)= 1/f(r) tinde spre infinit in dreptul valorilor de zero ale functiei f [exact ca in formulele Lorenz (a masei relativiste)].
[Dupa parerea mea, tocmai de aici deriva acest paradox al fortei de gravitatie infinite la distanta r=0, adica de la presupunerea ca forta de gravitatie se intinde la infinit ceea ce duce -ca si in exemplul rezolvat al grinzii infinite- la o ec. diferentiala cu solutii de forma sinusoidala. Paradoxul dispare daca renuntam la "distanta infinita".]
Acelasi lucru se intampla si in Fig. 9 si Fig. 13: G(r) tinde spre infinit la r= 0, din pricina anularii in O a functiei F(r). Cred ca nu se asteapta cineva ca in realitatea fizica sa apara acest infinit; ma refer aici in special la "masa relativista infinita" la viteza limita, "c", despre care se vorbeste cu seriozitate la fizica.
* Obs. - Desi am folosit diferite incarcari de grinzi, se constata ca dependenta care ne intereseaza -G(r)- nu este (practic) functie de inversul patratului distantei ci doar functie de inversul distantei [pe portiunile de curba ce ne intereseaza, cu "r" fff mic comparativ cu a. E de presupus, de aici pornind, ca o modelare mai buna poate fi obtinuta folosind o deformare a unei suprafete (si nu a unei axe). Este cazul placilor circulare incarcate cu o forta centrala concentrata (sau distribuita). Acestea beneficiaza in manuale de mai putina atentie decat grinzile deoarece apar mai putin frecvent in practica decat grinzile, calculul lor este mult mai complicat iar incercarile de laborator sunt mult mai putin dezvoltate la placi.
Se poate realiza distributia din Fig. 5 si ne putem imagina ca locul fiecarei sageti din figura va fi luat de niste mini-rachete a caror forta de propulsie este reglata sa fie proportionala cu marimea sagetii inlocuite.
Intrucat "rachetele" P si Q echilibreaza suma propulsiilor mini-rachetelor distribuite, ansamblul grinda+ rachete nu va avea miscare de translatie.
In schimb, datorita existentei perechilor in interactiune (acea "legatura" (brace) de care vorbeste B.H.), pot apare momente de rotatie. In spatiu doua corpuri ceresti se pot roti unul in jurul celuilalt tocmai datorita unui astfel de dezechilibru de momente. O asemenea grinda, aici, se va roti in planul fortelor, asemenea unei moristi si acest lucru se poate materializa si cu numai doua ajutaje paralele, montate pe o bara, indreptate in acelasi sens, cu forte de reactie diferite. Diferenta de forte va face din bara o morisca.
Problema este: care e mecanismul prin care ia nastere rotatia intr-o pereche? Aici se poate medita asupra cauzei...
2.3. Voi remedia neajunsul de la intrebarea (?7), pornind calculele de la capat, pe aceeasi Fig. 3+ 4, (devenite Fig. 3'+4'), cu modificarile:
- in locul celor doua cote "a", dintre capete si fortele concentrate, va fi 2a- r;
- in locul cotei dintre fortele concentrate, r= 2a va fi 2r;
- L= 4a (am lasat aceeasi lungime totala);
- in Fig.4 in locul fortelor concentrate din punctul 1, (2qa si qa), va fi o singura forta qr indreptata in sus;


Fig. 3'+ 4'
- Mred din Fig. 4' va fi: (20) Mred= -q(2a- r)2/2,
restul datelor de intrare ramanand neschimbate (daca nu specificam modificarile ar fi trebuit alte desene). Rezolvam la fel ca la paragrafele 2.2. si 2.1.,
(21) M1,2= Mred+ qrx- qx2/2 = -q(2a- r)2/2+ qrx- qx2/2
(22) d2v/dx2= -M1,2/EI= q(2a- r)2/2- qrx+ qx2/2= [(2a- r)2- rx+ x2/2]q/EI
(23) φ1,2= dv/dx= [(2a-r)2x/2 - rx2/2+ x3/6]q/EI+ C3
Din conditia de rotire zero, φ1,2=0, la mijlocul grinzii, x= r, rezulta prin inlocuire:
(24) C3= [2r3- 3r(2a- r)2]q/6EI
Putem calcula acum valoarea rotirii in nodul 1, pentru x=0 (deoarece avem intreaga ecuatie):
(25) φ1= C3= [2r3- 3r(2a- r)2]q/6EI
Ne mutam cu calculul pe portiunea A - 1:
(26) MA,1= - qx2/2; d2v/dx2= -MA,1/EI= +qx2/2EI
Integram pentru a obtine ec. rotirii si ec sagetii:
(27) φA,1= qx3/6EI+ C1 si
(27b) vA,1= qx4/24EI+ C1x+ C4
Gasim constanta de integrare C1 din conditia de continuitate a rotirii in nodul 1:
pentru x=2a- r, φ1,2= φ1= C3 si obtinem:
(28) C1= [2r3- 2(a+ r)(2a- r)2]q/6EI
Determinam constanta de integrare din conditia ca in nodul 1 sageata este zero, pentru x= 2a-r, pe care le inlocuim in ecuatia sagetii:
(29) C4= [-(2a- r)4- (2a- r)8r3+ 8(a+ r)(2a- r)3]q/24EI
In ecuatia sagetii, din conditia x= 0 rezulta valoarea sagetii (capatului de grinda, pe care o cautam prin acest calcul), care este egala cu termenul liber, C4.
(30) vA= C4= [-(2a- r)4- (2a- r)8r3+ 8(a+ r)(2a- r)3]q/24EI
In aceasta ecuatie putem da orice valori lui r deci putem trasa o curba a variatiei sagetii (in consecinta si a Energiei si a "Fortei") functie de distanta dintre cele doua reactiuni (de fapt echivalentele maselor din gravitatie). Ar trebui ca prin inlocuire cu r= a sa obtinem aceeasi valoare a sagetii ca in rezolvarea de la punctul 2.1. adica,
vA= 7qa4/24EI.
vA= [-(2a-a)4- (2a- a)8a3+ 8(a+ a)(2a- a)3]q/24EI= [-a4- 8a4+ 16a4]q/24EI= 7a4q/24EI,
adica acelasi rezultat ceea ce reprezinta o buna verificare a formulei si calculelor (in care usor se pierde un semn, o cifra, o litera, etc.). Acum putem determina/aprecia numeric aceasta variatie:
Pentru r=a, vA= 7[a4/24EI]= 7k;
r= 0,01a; vA= 48k;
r= 0,10a; vA= 47,31k;
r= 0,30a; vA= 42,23k;
r= 0,50a; vA= 34,53k
Intr-adevar, la o micsorare a distantei r de 10 ori, sageata nu creste de 100 ori (cat ar fi fost cu r2) ci numai de 6,7 ori.
(?10) E posibil sa fi gresit calculele/estimarile privind "forta" pe la sfarsitul paragrafului 2.2. si nu numai. Reiau de la ecuatia vA.
Lucrul mecanic efectuat de una din fortele "de reactie", qa, pe jumatate din valoarea sagetii din A, va fi:
(31) LA= qa*vA/2= qa*[-(2a- r)4- (2a- r)8r3+ 8(a+ r)(2a- r)3]q/48EI[/b]
Derivata lucrului mecanic va fi "forta" pe care o cautam:
(32) F= - dLA/dr= (4r3- 96ar2+ 144a2r)q2a/48EI
Valorile calculate -si comparate- de mai sus erau o estimare "prescurtata" ale "fortei", tinand cont ca in expresia lucrului mecanic doar v este variabila. Acum avem expresia matematica, functia, fortei F. In aceasta ecuatie ii dam lui "r" din nou aceleasi valori ca mai sus:
r= a; F= 52{q2a/48EI}= 52k;
r= 0,5a; F= 48,5k;
r= 0,3a; F= 34,7k;
r= 0,25a; F= 30k;
r= 0,1a; F= 13,4k;
r= 0,001a; F= 1,45k
* Aprecierile mele de mai sus erau usor gresite; situatia corect exprimata (si "neprescurtata"), exprimata sintetic, suna astfel: la micsorarea distantei r de 10 ori (de la a la 0,1a), inversul lui F (am mai amintit despre necesitatea inversarii acestui termen) va creste doar de ~4 ori.
* Arata mai rau decat ma asteptam; Este relativa alegerea valorii r ca referinta; Dependenta lui F de r este slaba (in comparatie cu dependenta cu 1/r2 de la gravitatie)
* Gradul trei al polinomului (al functiei de dependenta) nu are nici o semnificatie cat de cat in rezultatul final din pricina celorlalti termeni.
* Adevarul este ca distantele cosmice de interactie/actiune gravitationala/ pot fi foarte mari comparativ cu distanta intre 2 corpuri dintr-un sistem... Pentru ca sa ma situez in modelarea mea pe aproape trebuie sa folosesc valori mult, mult mai mici pentru r, comparativ cu a.
r= 0,0001a; F= 0,0144k;
r= 0,00001a; F= 0,00144k
Prin urmare, pe aceasta portiune de curba, singurul termen important din polinom devine 144a2r iar acesta are puterea I a lui "r" - distanta dintre "corpuri". E ceva mai bine si era de asteptat ca raportul dintre distanta r si lungimea totala a grinzii sa afecteze rezultatele modelarii.
* Apare inca o conditie: proportiile trebuie alese apropiate de cele gravitationale stiute.
[Teoria spune ca forta de atractie se intinde la infinit dar nimeni nu poate dovedi acest lucru, astfel ca pentru distante foarte mari (dar nu infinite) nici formula atractiei nu sufera abateri perceptibile.]
* Rezultatele sunt inca departe. Modelarea trebuie continuata cu grinda de lungime infinita. O aproximare (grosolana) a acesteia am inceput-o deja folosind "incarcarea triunghiulara".
4* Model: Grinda dreapta, simplu rezemata, cu incarcare triunghiulara


Fig. 6. [Gv]
In Fig. 6 avem un model ce aproximeaza actiunea unei forte concentrate pe mijlocul unei grinzi aflate pe un teren "moale", unde apare o reactiune distribuita de forma triunghiulara (aproximata in acest fel de mine). [Desenul arata inversat deoarece imi vine mai usor sa-l rezolv in aceasta pozitie rasturnata.]
(33) M1,2= - [(qx)*x/2]*x/3= -(qx/a)*x2/6= - qx3/6a;
Unde, (34) qx= qx/a, qx fiind valoarea sarcinii distribuite in punctul x, la distanta x de origine (capatul 1). Ecuatia fibrei medii deformate:
(34) d2v/dx2= - M1,2/EI= qx3/6a; Prin integrare obtinem ecuatia rotirii:
(35) φ1,2= - (q/6aEI)x4/4+ C1 ; Din conditia x= a; φ= 0, gasim valoarea constantei de integrare:
(36) C1= - qa3/24EI; Ecuatia rotirii e acum determinata:
(37) φ1,2= - (q/24aEI)x4- qa3/24EI; Prin integrare rezulta ec. sagetii:
(38) v1,2= (q/24aEI)x5/5- (qa3/24EI)x+ C2
Din conditia la limita, x=a; v=0, rezulta:
(39) C2= qa4/30EI. Cu aceasta, ecuatia sagetii devine:
(40) v1,2= (q/24aEI)x5/5- (qa3/24EI)x+ qa4/30EI= (q/120aEI)[x5- 5a4x+ 4a5]
Inlocuim variabila x cu (a-r) in ecuatia sagetii pentru a obtine aceeasi sageata, din punctul "curent", dar ca si functie de "r". Dupa cum se vede din Fig.6, aceasta distanta r dintre aplicatiile a doua forte (egale) este aceea care ne intereseaza (si, in final vom studia variatia lui r, valoric).
(41) vr= (q/120aEI)[(a-r)5- 5a4(a- r)+ 4a5]
Energia potentiala, egala cu lucrul mecanic efectuat de catre una din incarcarile qa, deplasandu-se vertical pe distanta vr, este:
(42) ΔE= L= qavr Forta pe care o cautam, echivalentul celei gravitationale:
(43) F= - dE/dr= (q2/120EI)(5r4- 20ar3+ 30a2r2- 20a3r)= (q2/24EI)( r4- 4ar3+ 6a2r2- 4a3r)
Verificare:
In ecuatia (40), sageata ca functie de x,
- pentru x=r trebuie sa rezulte sageata zero (caci reazemul e fix); Prin inlocuire in (40):
v1,2= (q/120aEI)[r5- 5a4r+ 4a5]= 0; Corect!
- pentru x= 0 trebuie sa avem sageata maxima, v≠ 0; Prin inlocuire, primii doi termeni din paranteza se anuleaza si obtinem:
v1,2= (q/120aEI)[ (0)5- 5a4*(0)+ 4a5]= qa4/24EI≠ 0 ; Corect!
In ecuatia (41), sageata functie de r,
- pentru r= 0, ar trebui sa rezulte sageata zero; Inlocuim in ec. (41) si obtinem:
vr= (q/120aEI)[(a-0)5- 5a4(a- 0)+ 4a5]= (q/120aEI)[a5- 5a4a+ 4a5]= 0; Corect!
- pentru r= a, pe capatul grinzii ar trebui sa rezulte o sageata diferita de zero. Inlocuim in ec. (41) pe r cu a, primii doi termeni se anuleaza, si obtinem:
vr= (q/120aEI)[(a-a)5- 5a4(a- a)+ 4a5]= qa4/24EI≠ 0; Corect!
In ec. (43) a derivatei, pentru r= 0, derivata se anuleaza, cum era si normal [caci derivata intai e tangenta la curba si aici, pe reazem, -stim din RM- unghiul tangentei la fibra deformata e zero] iar in aceeasi ec. (43) inlocuind r=a, rezulta o derivata diferita de zero [corespunzand cu ce stim apriori din RM- ca tangenta la curba este diferita de zero]
A trebuit sa ma asigur ca ecuatiile obtinute sunt exacte deoarece la calculele de acest tip apar nenumarate greseli algebrice, din neatentie, din cauza specificului, si - cateodata- din nestiinta. Acum putem da valori numerice (in ec. 43) pentru r cu scopul trasarii diagramei (alta verificare):
r= a; F= -(q2/120EI)5a4= -q2a4/24EI= -k ;
r= 0,8a; F= -0,998k
r= 0,6a; F= -0,974k
r= 0,5a; F= -0,9375k;
r= 0,4a; F= -0,8404k;
r= 0,3a; F= -0,768k;
r= 0,2a; F= -0,592k;
r= 0,1a; F= -0,364k;
r= 0,01a; F= -0,0394k;
r= 0,001a; F= -0,00399k;
r= 0,0001a; F= -0,000399k;
r= 0,00001a; F= -0,0000399k; etc.
Si de aceasta data, la un raport r/a apropiat de cel cosmic, "F" este proportionala cu "r" (la o scadere de 10 ori a lui r, F scade tot de 10 ori). Deci F nu e proportionala cu patratul lui "r", adica patratul distantei dintre punctele de aplicare a sarcinilor.
Ma incurca semnul minus, despre care nu stiu cum a aparut...
5* Model: Grinda de lungime infinita pe mediu elastic


Fig. 7.
Grinda asezata pe un mediu elastic este o grinda static nedeterminata.
Mediul, terenul pe care este asezata grinda se considera perfect elastic, adica el coboara sub sarcina si revine dupa inlaturarea sarcinii. E cazul sinelor de cale ferata.
Se considera ca reactiumea din dreptul unei sectiuni oarecare a grinzii, pe care terenul o exercita asupra grinzii, este proportionala cu sageata grinzii din dreptul sectiunii respective (ipoteza E. Winkler). Astfel, reactiunea pe o unitate de lungime a grinzii este:
p= -kv
, unde k e coeficientul de tasare, modul de fundatie, sau coeficient de rigiditate si el depinde numai de natura terenului. k>10 pentru teren stancos si k<10 pentru teren nisipos, argilos, cu pietris, loess, etc.Rezolvarea acestei grinzi, cu o forta concentrata P, este data in manualul de RM al prof. Ioan Deutsch, de unde aflam ecuatia sagetii v la distanta x de punctul de aplicatie al fortei concentrate:
(44) vx= e-βx(cosβx+ sinβx)P/(8β3EI)
Cu aceasta formula -pe principiul suprapunerii efectelor- putem calcula energia potentiala, inmagazinata de grinda, egala cu lucrul mecanic produs de o a doua forta P, -situata la distanta r (x in formula 44) de prima forta P- ce se deplaseaza pe o distanta egala cu sageata produsa de prima forta P (sau viceversa). [In exemplul numeric din manual, fortele aplicate nu sunt identic egale dar sunt apropiate valoric deci putem folosi forte diferite.]
(45) E= L= Pvr
Forta pe care o cautam e derivata energiei:
(46) F= -dE/dr= P2e-βrsinβr/(4β2EI)
Pe aceasta formula putem determina forma curbei de dependenta, F(r), dand valori lui r. Din pacate nu putem decat presupune valorile coeficientului β. La sinele de cale ferata, in exemplul din manual, produsul βr= 0,742, deci e subunitar. Asta inseamna ca valoarea coeficientului β este comparabila cu distanta r.
A trasa diagrama F(r) e sinonim cu a trasa functia: f= sinβr/eβr
Presupunem β= 0,0053 cm-1
r= 10 cm; βr= 0,053; f= 0,0502;
r= 14 cm; βr= 0,0742; f= 0,069;
r= 100 cm; βr= 0,530; f= 0,297;
r= 140 cm; βr= 0,742; f= 0,238;
r= 500 cm; βr= 2,65; f= 0,033;
r= 600 cm; βr= 3,18; f= -0,0015;
r= 1000 cm; βr= 5,3; f= -0,004;
r= 1200 cm; βr= 6,36; f= 0,00013;
r= 14000 cm; βr= 7,42; f= 0,000543;
Nu am fost prea atent caci aceasta curba era deja trasata in manualele de RM si arata astfel:


Fig. 8.
Functia f este η3 din diagrama.
Problema care apare aici este legata de constatarea ca pentru r=0 functia f=0= kF. Intrucat F ar trebui sa fie modelul fortei de atractie gravitationale, atunci nu se potriveste de loc cu valorile obtinute [in sensul ca "forta" ar trebui sa fie maxima tocmai la r= 0]. Problema aceasta provine din faptul ca am neglijat aspectul/neajunsul enuntat in intrebarile ?1 si ?2. Incerc sa rezolv acest aspect:
Atat in formula (5) de la Modelul 1. cat si in formulele (19) si (32) de la Modelul 2. dar si in formula (43) de la Modelul 3. persista aceasta nepotrivire. Toate aceste formule pot fi sintetizate intr-o singura formula astfel:
(47) F= P*Q*f(r)/k; Putem inversa aceasta relatie:
(48) 1/F= k(1/P)*(1/Q)*(1/f(r)); Facem urmatoarea notatie: 1/F= G; 1/P= M1; 1/Q= M2 si vom obtine urmatoarea relatie (aproape identica cu formula atractiei gravitationale):
(49) G= kM1*M2*(1/f(r))
Daca numitorul f(r) ar fi x2 atunci formal ar fi vorba despre aceeasi formula si modelul ar fi perfect viabil. Pana acum nu am indeplinit inca ultima cerinta: f(r), care uneori e un polinom de gradul 2 in x sau de alt grad, adica nu are forma unui monom, x2. Chiar si cu polinoame, dependenta ce o cautam e ~liniara de grd. I (pe portiunea din curba ce ne intereseaza, la un anume raport r/a).
Ceea ce nu am analizat pana acum este anularea in origine la formula (46) [si la (43), (32), si (19), mai putin la formula (5)] ceea ce este echivalent cu
G= ∞, adica exact cum se intampla in formula gravitatiei [atunci cand r= 0, forta de atractie gravitationala tinde spre ∞]. Sa fi gresit ceva in formula (5)...?
De remarcat ca, in Fig.8, η3 e singura care se anuleaza in origine.
De la sine apare observatia -chiar daca nu are legatura cu modelul nostru- ca valorile folosite in practica (momentul de inertie al sinelor de cale ferata, coeficientul de tasare, coeficientii) conduc la situarea problemei pe curba η3 exact in punctul ei de minim ceea ce nu poate fi o intamplare. Sa fie explicatia ca acolo e "punctul slab" si toate masurile sunt luate pentru dimensionare special pentru zona aceea?...
(?11) Rezultatele formulelor (19) si (32) nu coincid. Trebuie lamurit de ce "nu".
Reprezentarea grafica a functiilor, determinate in cadrul celor catorva modele, poate ajuta la vizualizarea legaturii, la gasirea eventualelor greseli de calcul numeric, la verificare in general, prezentare sintetica de rezultate, etc., fiind si una din cele mai frecvent folosite metode ingineresti. Am reprezentat functia F cat si inversa ei, G. Scarile alese sunt aleatorii pentru fiecare curba trasata.
Fig. 9.?


[F. 10 Gv]

Fig.10. [F. 11 Gv]


Fig.12. [Gv]


Fig.13. [Gv]
Fig. 9 (si 12) se refera la Modelul 2*, Fig. 10 se refera la Modelul 5* iar Fig 13 se refera la Modelul 4*. Fig. 12 este o repetare "mai artistica" a Fig. 9.
In Fig. 10 se confirma forma de sinusoida amortizata a functiei f. Functia g(r)= 1/f(r) tinde spre infinit in dreptul valorilor de zero ale functiei f [exact ca in formulele Lorenz (a masei relativiste)].
[Dupa parerea mea, tocmai de aici deriva acest paradox al fortei de gravitatie infinite la distanta r=0, adica de la presupunerea ca forta de gravitatie se intinde la infinit ceea ce duce -ca si in exemplul rezolvat al grinzii infinite- la o ec. diferentiala cu solutii de forma sinusoidala. Paradoxul dispare daca renuntam la "distanta infinita".]
Acelasi lucru se intampla si in Fig. 9 si Fig. 13: G(r) tinde spre infinit la r= 0, din pricina anularii in O a functiei F(r). Cred ca nu se asteapta cineva ca in realitatea fizica sa apara acest infinit; ma refer aici in special la "masa relativista infinita" la viteza limita, "c", despre care se vorbeste cu seriozitate la fizica.
* Obs. - Desi am folosit diferite incarcari de grinzi, se constata ca dependenta care ne intereseaza -G(r)- nu este (practic) functie de inversul patratului distantei ci doar functie de inversul distantei [pe portiunile de curba ce ne intereseaza, cu "r" fff mic comparativ cu a. E de presupus, de aici pornind, ca o modelare mai buna poate fi obtinuta folosind o deformare a unei suprafete (si nu a unei axe). Este cazul placilor circulare incarcate cu o forta centrala concentrata (sau distribuita). Acestea beneficiaza in manuale de mai putina atentie decat grinzile deoarece apar mai putin frecvent in practica decat grinzile, calculul lor este mult mai complicat iar incercarile de laborator sunt mult mai putin dezvoltate la placi.
Ultima editare efectuata de catre mm in Mar Feb 18, 2020 11:31 am, editata de 5 ori
mm- Mesaje : 211
Data de înscriere : 12/01/2011
 Modelarea Gravitatiei, in Rezistenta Materialelor, pe o placa (plana), central incarcata, solicitata la incovoiere.
Modelarea Gravitatiei, in Rezistenta Materialelor, pe o placa (plana), central incarcata, solicitata la incovoiere.
6* Model: Placa plana, simplu rezemata pe contur, incarcata cu forta concentrata centrala
Din aproape in aproape, prin modelari succesive, am ajuns la concluzia ca modelul cu grinda nu ne da o dependenta de r-2 a fortei, forta pe care o calculam din considerente energetice. Dar este posibil ca sa gasim aceasta dependenta la placi.
Placa circulara, incarcata cu o forta centrala, concentrata, este rezolvata in cartile de RM si putem prelua direct formulele din rezolvare. Sa analizam putin acest caz.
In manualul de RM a prof. I. Deutsch gasim rezolvarea acestei placi cu solutiile:
(50) φP= Pr[ln(R/r)+ 1/(1+ µ)]/8πr
(51) vP= P[r2ln(r/R)+ (3+ µ)(R2- r2)/2(1+ µ)]/16πR
Forta P este centrala, rezemarea placii se face pe un cerc de raza R, cu originea in punctul de aplicare al fortei concentrate P. In ec. (51) alegem o valoare η= r/R= 0,1 si consideram µ= 0,3 (pentru otel) deocamdata, cu rezerva ca in eter acesta ar putea avea o alta valoare. Si rezulta:
(52) vP= (1,27R2- 3,57r2)P/16πR
Diferenta de energie, ca si in cazurile precedente, ΔE= L= QvP;
Forta, F= -dE/dr. Unde Q este tot o forta concentrata, aflata pe aceeasi placa la distanta r de forta P si care va efectua un lucru mecanic pe distanta vP.
(53) F= 0,142(PQ/R)r
In sfarsit am gasit o dependenta curata a sagetii, numai de r2. Din pacate, in ecuatia fortei F acest patrat se reduce prin derivare la un simplu r.
Deci ne-ar fi fost util un model cu o sageata dependenta doar de r3 insa acest lucru nu pare sa rezulte de la cele 8 modele de placi plane pe care le gasim in manual.
Ramane speranta ca un model de placa infinita rezemata pe o suprafata elastica ar putea sa fie o rezolvare mai buna a problemei propuse aici spre rezolvare.
Sau, un model spatial, volumic, incarcat central insa nu-mi pot imagina cum ar arata fizic un asemenea model.
Poate ca am simplificat problema prea mult...
(54) F= - Q*vP'= PQ[r2ln(r/R)+ (3+ µ)(R2- r2)/2(1+ µ)]'/16πR= - PQ(r2lnr- r2lnR+ kR2- kr2)'k1= - k1PQ(2rlnr+ r- 2rlnR- 2rk)= - k1[2rlnr + r(1- 2lnR- 2k)]
Unde gradul celui de-al doilea termen din paranteza este clar, unu. Fiind mai greu de apreciat ce grad are termenul "2rlnr", am folosit descompunerea in serie a lui lnr:
lnr= 2[(r- 1)/(r+ 1) + 1/3(r- 1)3/(r+ 1)3],
din care am luat in considerare numai primii doi termeni ai dezvoltarii. Facand calculele algebrice, am obtinut pentru termenul 2rlnr expresia:
2rlnr= 16r(r3- 1)/3/(r+ 1)3, expresie care este si ea de grd. I.
Prin urmare, gradul intai in "r" pentru intreaga expresie a lui F. Nu prea ma asteptam la un asemenea rezultat.
mm- Mesaje : 211
Data de înscriere : 12/01/2011
Pagina 1 din 1
Permisiunile acestui forum:
Nu puteti raspunde la subiectele acestui forum|
|
|


